A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
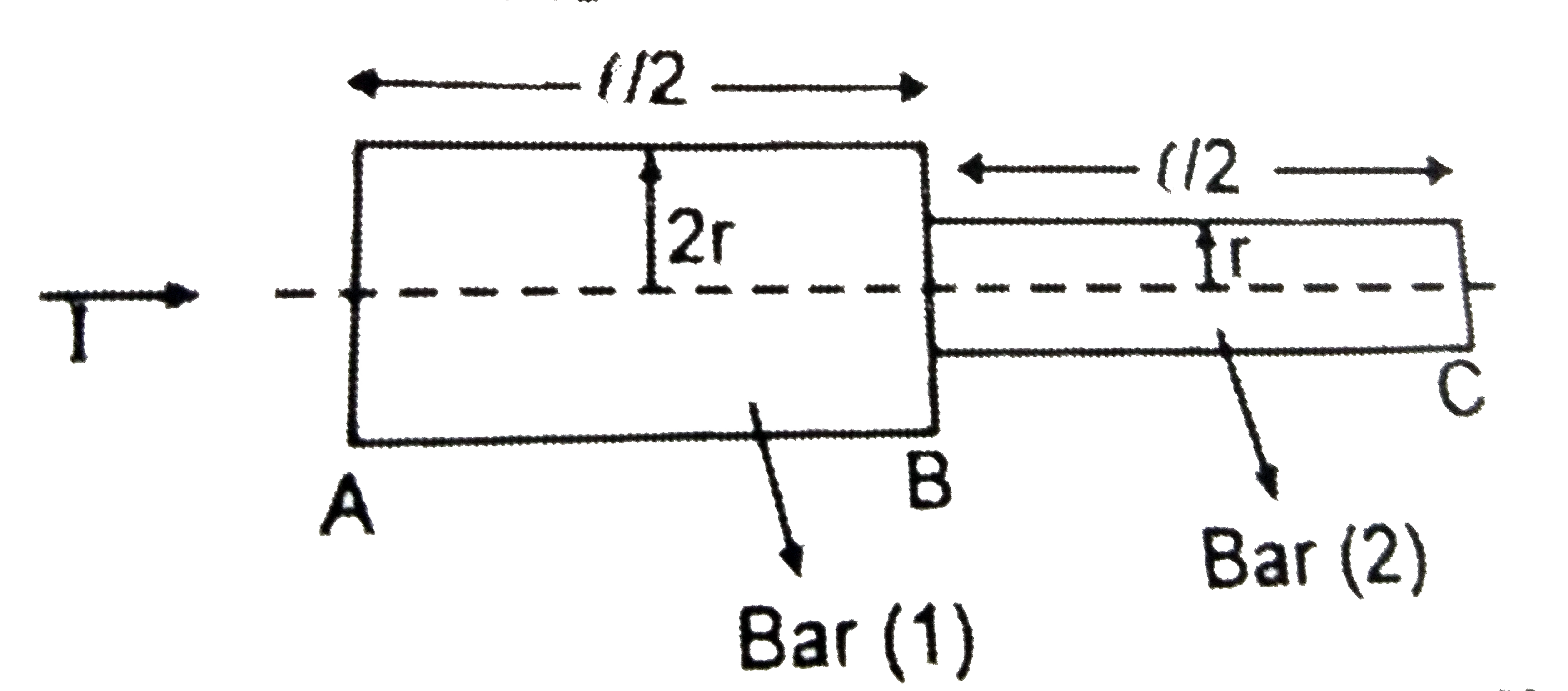
- Two bars of equal resistivity rho and radius 'r' and '2r' are kept in ...
Text Solution
|
- Two bars of radius r and 2r are kept in constant as shown in figure. A...
Text Solution
|
- A current i passes through a wire of length l , radius of cross-sectio...
Text Solution
|
- Two bars of equal resisttivity rho and radil 'r' and '2r' are kept in ...
Text Solution
|
- Two wires having resistances R and 2R are coneected in series . If cu...
Text Solution
|
- Two wires having resistances R and 2R are coneected in parallel . If...
Text Solution
|
- A tapered bar of length L and end diameters D(1) and D(2) is made of a...
Text Solution
|
- A tapered bar of length L and end diameters D1 and D2 is made of mater...
Text Solution
|
- दो दंड जिनकी त्रिज्याएँ क्रमश: r तथा 2r है, चित्रानुसार संपर्क में है|...
Text Solution
|