Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
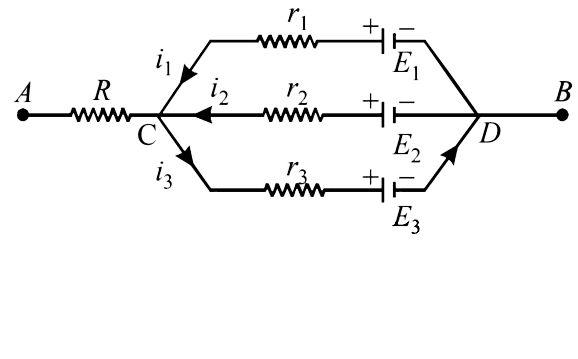
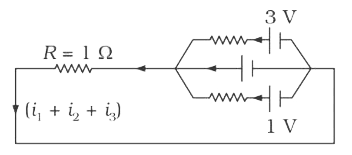
- In the circuit shown in fig E1 = 3 volts, E2 = 2volts, E3 = 1volt and ...
Text Solution
|
- In the circuit shown in fig E1 = 3 volts, E2 = 2volts, E3 = 1volt and ...
Text Solution
|
- In the circuit in figure E1=3V, E2=2V, E3=1V and R=r1-r2-r3=1Omega a. ...
Text Solution
|
- Calculate the current through each resistance in the given circuit. Al...
Text Solution
|
- In the following circuit ,E1 = 4V, R1 = 2 Omega, E2 = 6 V, R2 = 2Oem...
Text Solution
|
- In the circuit shown in fig. 5.265, E1 = E2 = E3 = 2V and R1 = R2 = 4O...
Text Solution
|
- For the batteries shown in fig. R1, R2 and R3 are the internal resista...
Text Solution
|
- चित्र में E1 " व " E2 क्रमश: 2.0 वोल्ट व 4.0 वोल्ट है , तथा प्रतिरोध r...
Text Solution
|
- For the circuit shown, with R1=1.0 Omega,R2=2.0Omega,E1=2V and E2=E3...
Text Solution
|