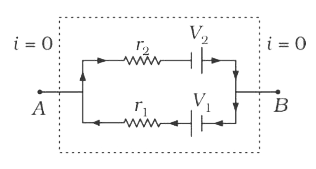
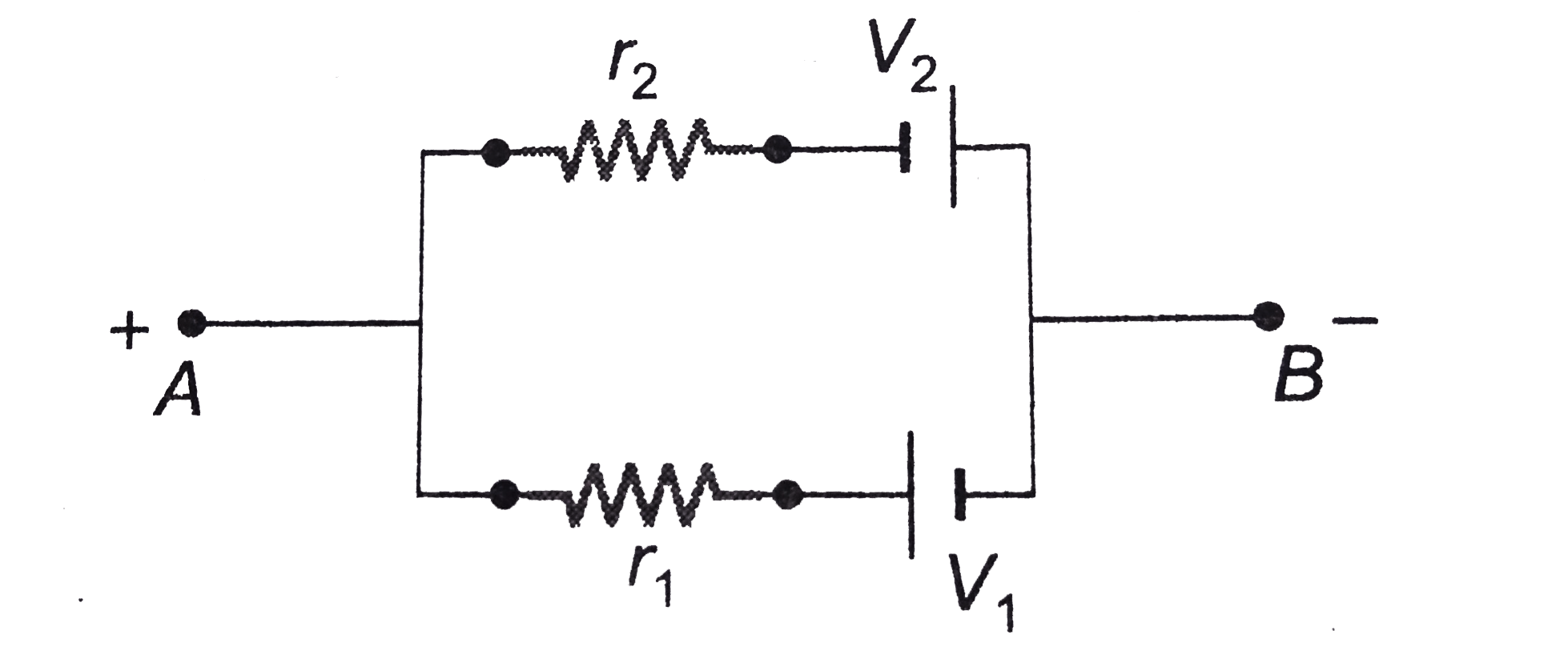Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the emf (V) and internal resistance (R) of a single battery which...
Text Solution
|
- Two ideal batteries of emf V1 and V2 and three resistances R1, R2 and ...
Text Solution
|
- Find the emf and internal resistance of a single battery which is equi...
Text Solution
|
- In the circuit shown in figure a 12 V battery with unknown internal re...
Text Solution
|
- Find the emf ( V ) and internal resistance (R) of a single battery whi...
Text Solution
|
- find the emf (epsi(0)) and internal resistance (r(0)) if a battery whi...
Text Solution
|
- Two cells of emf E1.E2 and internal resistance r1 , r2 respectively ar...
Text Solution
|
- Find the emf (V) and internal resistance (r) of a single battery which...
Text Solution
|
- Two batteries of emfs 2 V and 1 V of internal resistances 1Omega and 2...
Text Solution
|