A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
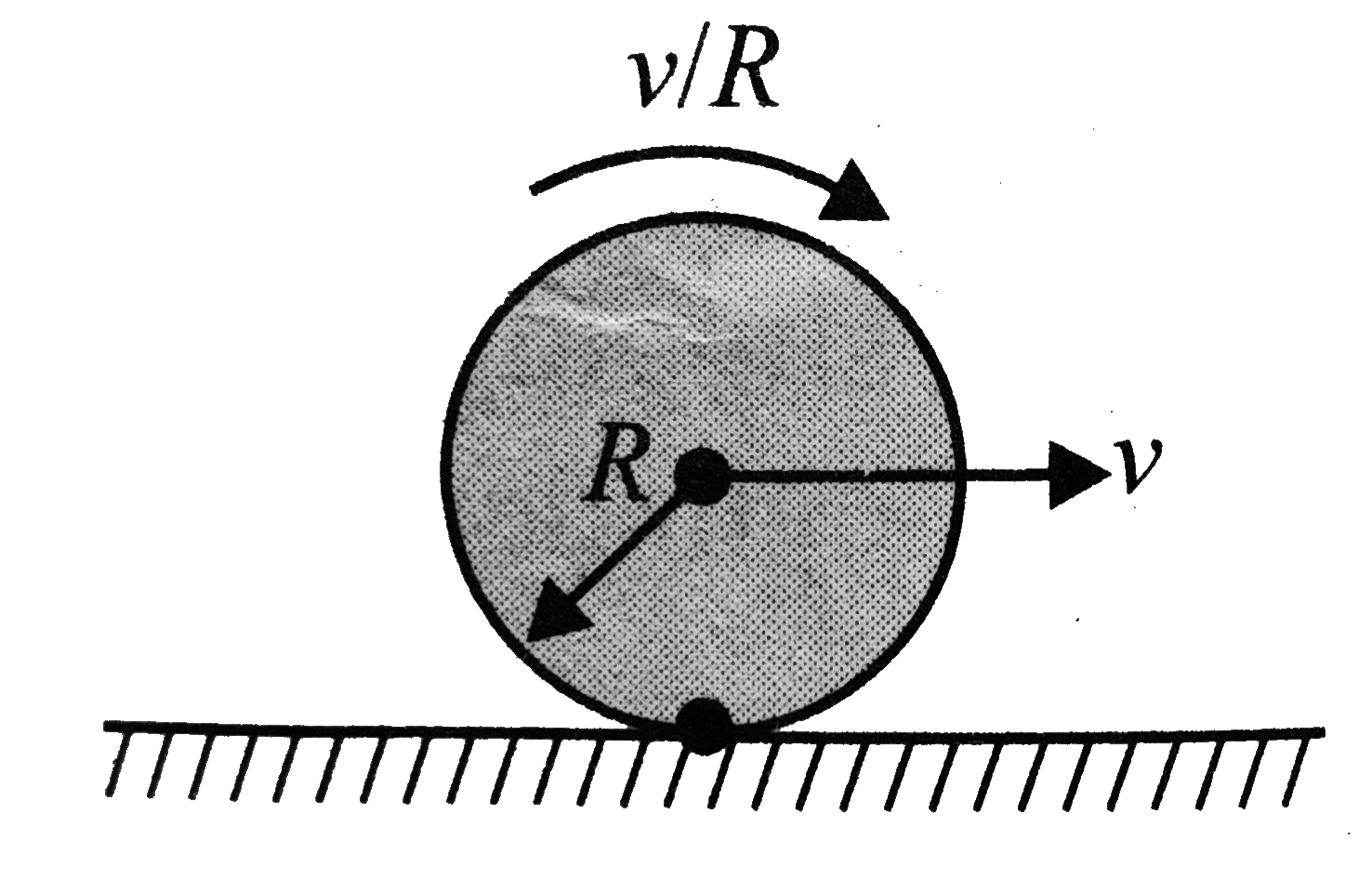
- A disc is performing pure rolling on a smooth stationary surface with ...
Text Solution
|
- A disc of radius R is rolling purely on a flat horizontal surface, wit...
Text Solution
|
- the disc of the radius r is confined to roll without slipping at A an...
Text Solution
|
- A disc of radius R rolls on a horizontal ground with linear accelerati...
Text Solution
|
- A disc is performing pure rolling on a smooth stationary surface with ...
Text Solution
|
- A disc of radius R is rolling without sliding on a horizontal surface ...
Text Solution
|
- A disc of radius R is rolling purely on a flat horizontal surface, wit...
Text Solution
|
- A disc is rolling without sliding on a horizontal surface. Velocity of...
Text Solution
|
- As shown in the figure, a disc of mass m is rolling without slipping w...
Text Solution
|