Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
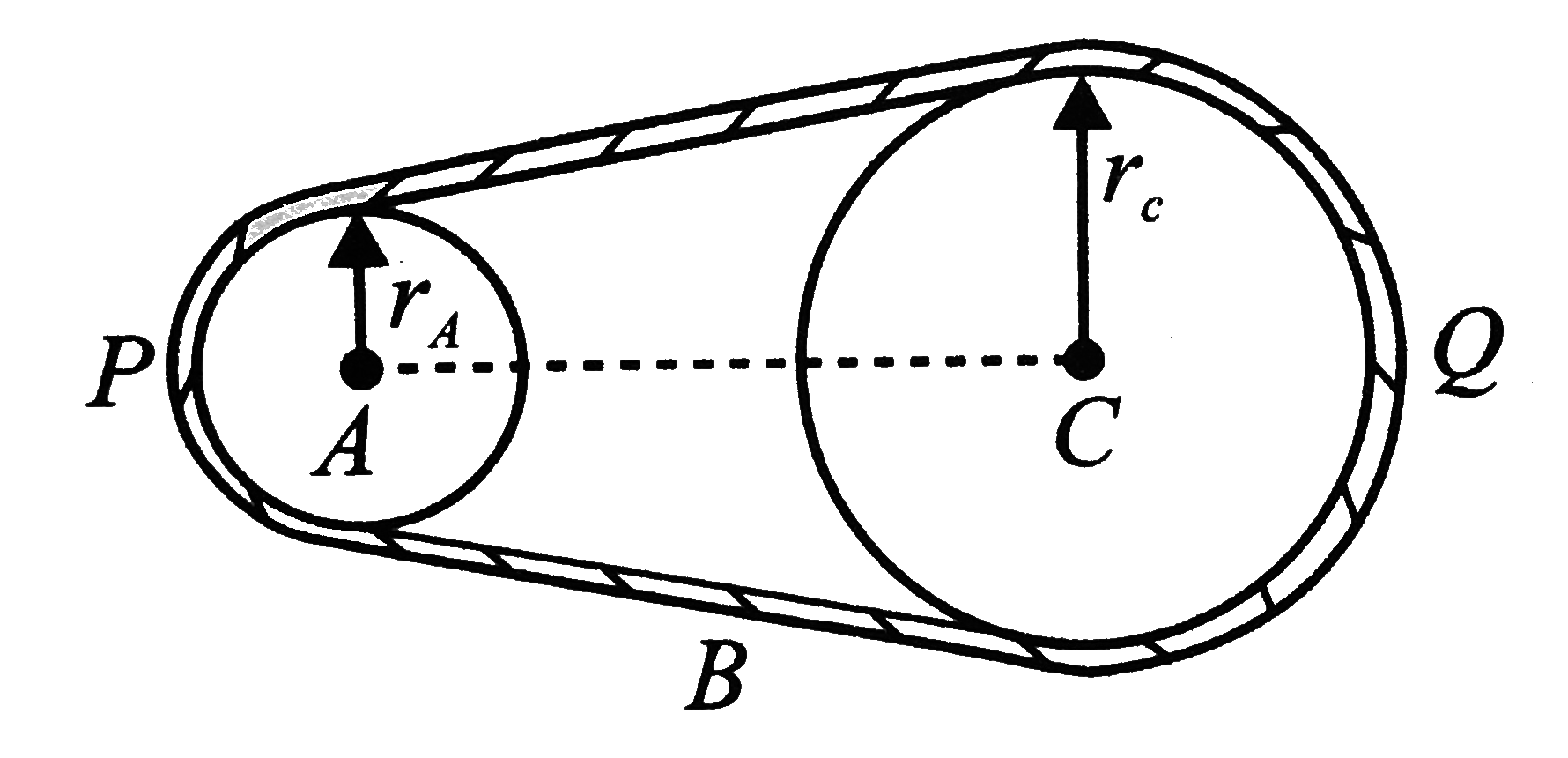
- Two wheels A and C are connected by a belt B as shown in figure. The r...
Text Solution
|
- Two rigid bodies A and B rotate with angular momenta L(A) and L(B) res...
Text Solution
|
- Two wheels A and C are connected by a belt B as shown in figure. The r...
Text Solution
|
- Wheels A and B in Figure are connected by a belt that does not slip. T...
Text Solution
|
- घूर्णन करने वाली दो वस्तुओं A व B के जड़त्व आघूर्ण I(A) व I(B)(I(A)gtI...
Text Solution
|
- दो वस्तुओं A व B के जड़त्व आघूर्ण I(A) व I(B) (I(A) gtI(B)) हैं। यदि इ...
Text Solution
|
- A wheel of mass 10 kg and radius of gyration 50 cm is rotating at 300 ...
Text Solution
|
- A wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt...
Text Solution
|
- चित्र में A और B दो पहिये हैं, जो एक ही बेल्ट द्वारा जुड़े हुए हैं । B ...
Text Solution
|