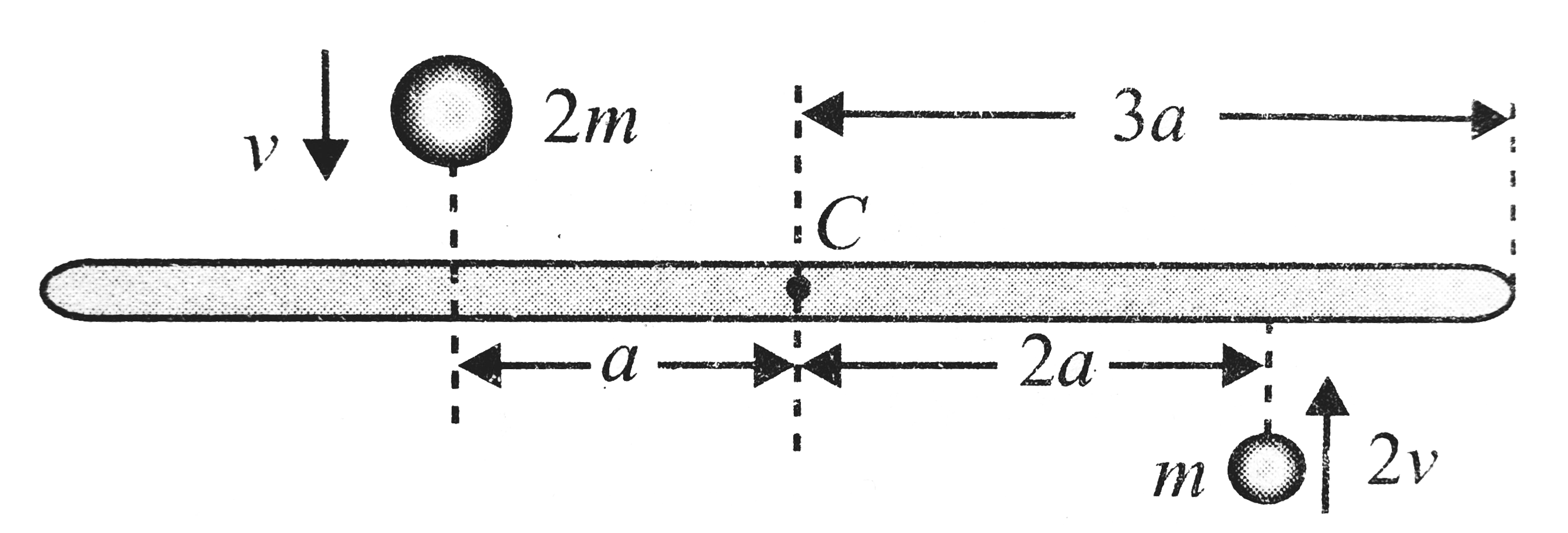
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform bar of length 6a and mass 8m lies on a smooth horizontal tab...
Text Solution
|
- A uniform rod of mass M and length a lies on a smooth horizontal plane...
Text Solution
|
- A uniform bar of length 6a and mass 8m lies on a smooth horizontal tab...
Text Solution
|
- A uniform bar of length 6a and mass 8m lies on a smooth horizontal tab...
Text Solution
|
- A uniform rod of length L lies on a smooth horizontal table. The rod h...
Text Solution
|
- A uniform bar of length 6a and mass 8m lies on a smooth horizontal tab...
Text Solution
|
- A uniform bar of length 6a and mass 8 m lies on a smooth horizontal ta...
Text Solution
|
- A thin uniform bar of length L and mass 8m lies on a smooth horizontal...
Text Solution
|
- A bar of mass m and length l is in pure translational motion with its ...
Text Solution
|