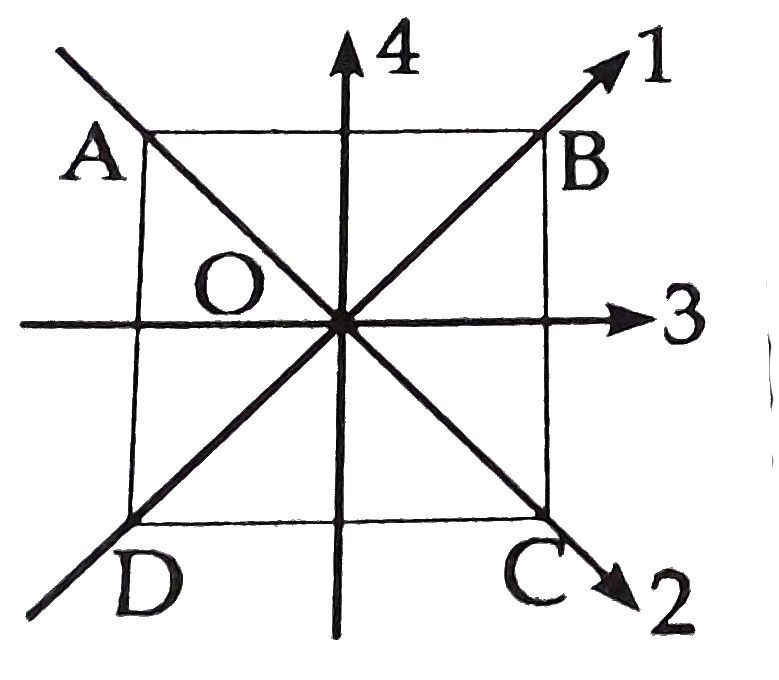
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The moment of inertia of a thin square plate ABCD of uniform thickness...
Text Solution
|
- Consider a uniform square plate of of side and mass m. The moment of i...
Text Solution
|
- I is moment of inertia of a thin square plate about an axis passing th...
Text Solution
|
- If I moment of inertia of a thin circular plate about an axis passing ...
Text Solution
|
- The moment of inertia of a thin square plate ABCD of uniform thickness...
Text Solution
|
- The moment of inertia of a thin square plate ABCD of uniform thickness...
Text Solution
|
- Consider a uniform square plate of side 'a' and mass 'm'. The moment o...
Text Solution
|
- Consider a uniform square plate of side 'a' and mass 'm'. The moment o...
Text Solution
|
- एक समान मोटाई की पतली वर्गाकार प्लेट ABCD का तल ले लंबवत तथा केंद्र O ...
Text Solution
|