Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
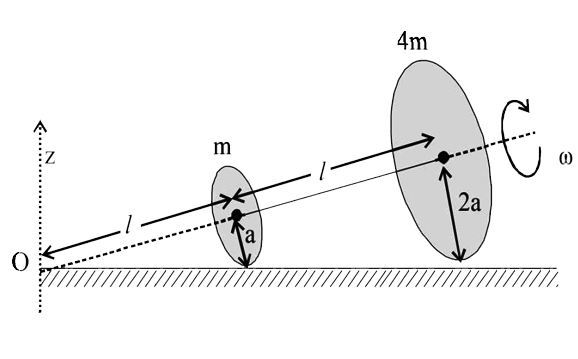
- Two thin circular discs of mass m and 4m, having radii of a and 2a, re...
Text Solution
|
- Two thin circular discs of mass m and 4m, having radii of a and 2a, re...
Text Solution
|
- Three equal masses m are rigidly connected to each other by massless r...
Text Solution
|
- A thin uniform rod of length l and mass m is swinging freely about a h...
Text Solution
|
- Two point masses A of mass M and B of mass of 4M are fixed at the ends...
Text Solution
|
- A uniform rod of mass m and length L is fixed to an axis, making an an...
Text Solution
|
- A uniform rod of mass m and length L lies radialy on a disc rotating w...
Text Solution
|
- Find the centers of two thin circular discs of mass m and 4m whose rad...
Text Solution
|
- A thin uniform rod of mass M and length L is rotating about a perpendi...
Text Solution
|