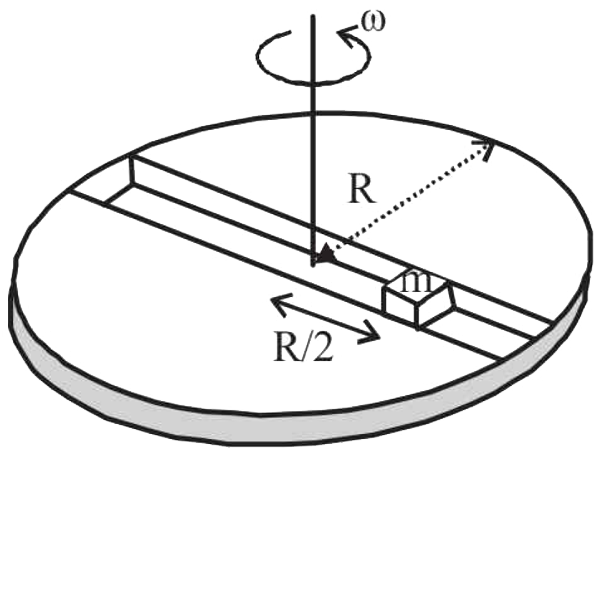
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A frame of reference that is accelerated with respect to an inertial f...
Text Solution
|
- NON-INERTIAL FRAME OF REFERENCE
Text Solution
|
- A frame of reference that is accelerated with respect to an inertial f...
Text Solution
|
- A frame of reference that is accelerated with respect to an inertial f...
Text Solution
|
- Assertion : A reference frame attached to earth is an inertial frame...
Text Solution
|
- In an inertial frame of reference, the magnetic force on a moving char...
Text Solution
|
- Distinguish between inertial and non-inertial frames of reference.
Text Solution
|
- Define inertial and non-inertial frames of reference with example.
Text Solution
|
- Define inertial frame and non-inertial frame. Is earth an inertial fra...
Text Solution
|