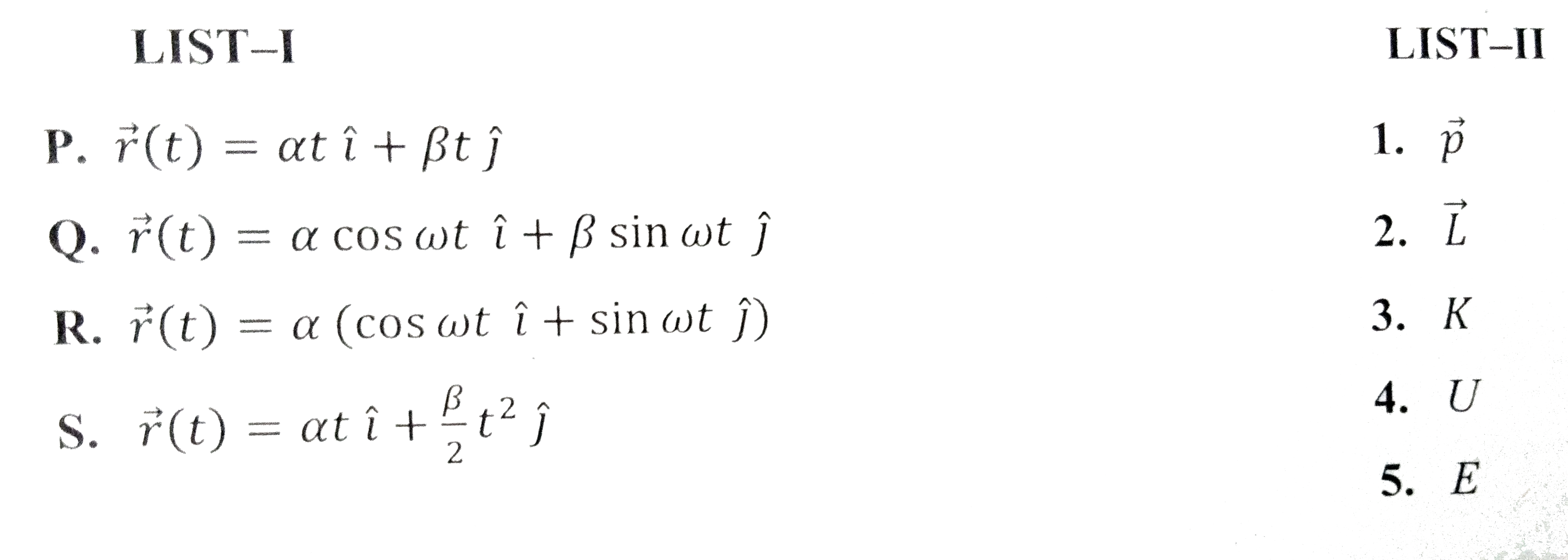A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the List-I below, four different paths of a particle are given as f...
Text Solution
|
- A particle has a linear momentum p and position vector r. the angular ...
Text Solution
|
- In the List-I below, four different paths of a particle are given as f...
Text Solution
|
- The linear momentum p of a particle is given as a function of time t a...
Text Solution
|
- The linear momentum of a particle as a fuction of time 't' is given by...
Text Solution
|
- Starting from the definition of angular momentum in terms of position ...
Text Solution
|
- Torque acting on a particle about an arbitrary origin is zero, What ca...
Text Solution
|
- A particle is going around in a circular path with constant speed. Ang...
Text Solution
|
- नीचे दी गयी सूची-1 में, एक कण के चार विभिन्न पथ, समय के विभिन्न फलनों ...
Text Solution
|