Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A small sphere rolls down without slipping from the top of a track in ...
Text Solution
|
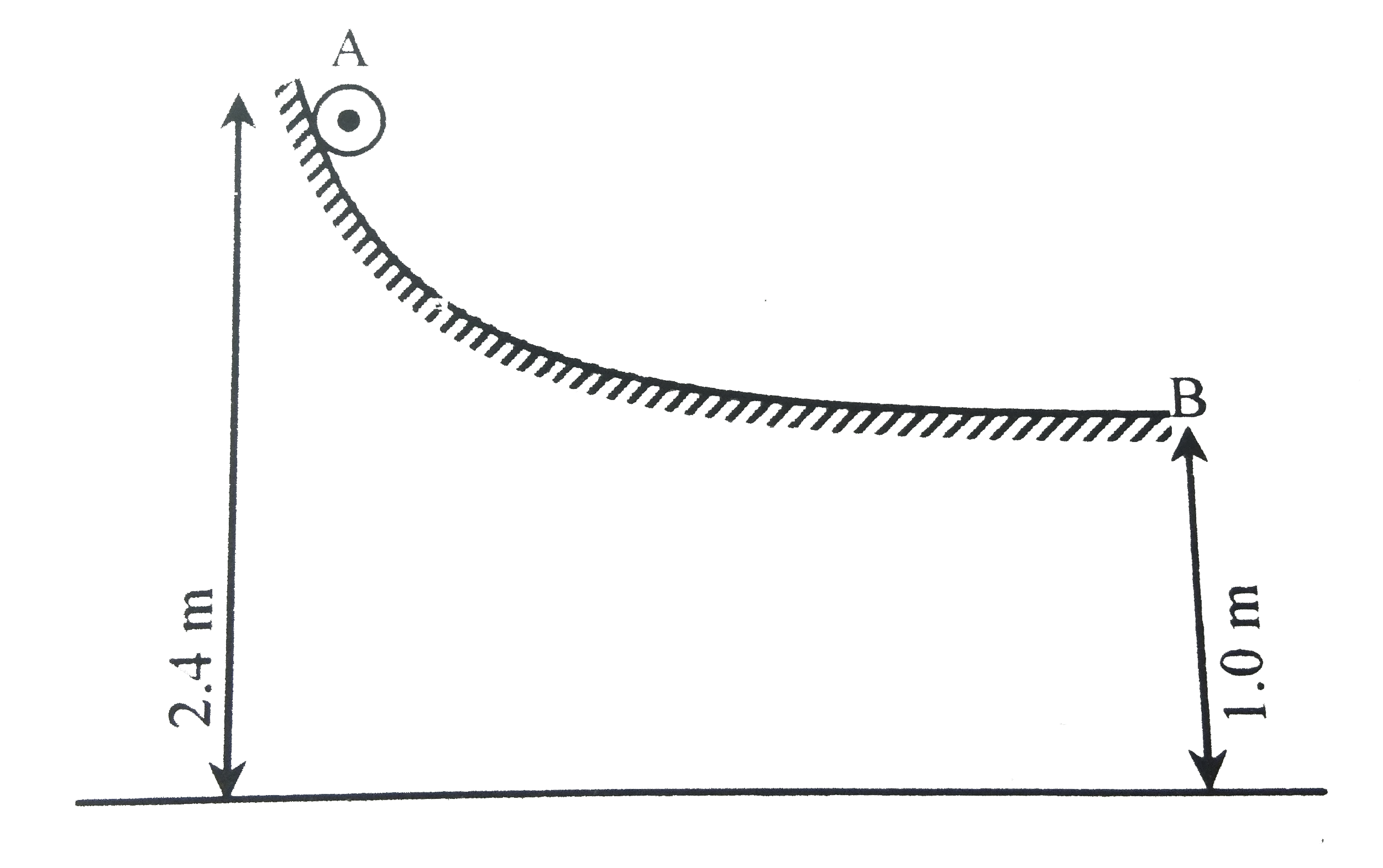
- Figure shows a particle slideing on a frictionles track which terminat...
Text Solution
|
- A small sphereical ball is released from a point at a height h on a ro...
Text Solution
|
- A small sphere rolls down without slipping from the top of a track in ...
Text Solution
|
- A small sphere rolls down without slipping from the top of a track in ...
Text Solution
|
- The figure shown a particle sliding on a frictionless track, which tem...
Text Solution
|
- A disc of radius r = 0.1 m is rolled from a point A on a track as show...
Text Solution
|
- Two poles of height 6 meters and 11 meteras stand vertically on a plan...
Text Solution
|
- Figure shows a loop track whose lower part ends into a circular track ...
Text Solution
|
 .
. 