(i) `(12V)/(7L)`, (ii) `35 ms^(-1)`

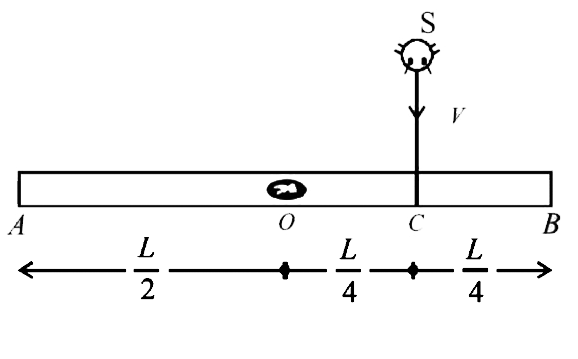
Let us take rod insect as a system. There is not external impulse acting on the system. Hence, we can apply conservation of angular momentum just before and just after collision about the point O. Angular momentum of the system before collision = angular momentum of the system after collision.
`MV xx L/4 = Iomega`
Where I is the moment of inertia of the system just after collision and `omega` is the angular velocity just after collision.
`rArr MV xx L/4 = [M (L/4)^(2) + 1/12 ML^(2)]omega`
`rArr MV xx L/4 =(ML^(2))/4[1/4 +1/3] omega = (ML^(2))/4[(3+4)/12]omega = (ML^(2))/4 xx 7/12 xx omega rArr omega = 12/7 xx V/L`.
Initially the rod was in equilibrium. But after collision there is an extra mass M of the insect which creates a torque in the clockwise direction, which tries to create angular acceleration in the rod. But the same is compensated by the movement of insect towards B due to which moment of inertia of the system increase.
Let at any instant of time t the insect be at a distance x from the centre of the rod and the rod has turned through an angle `theta(=omegat)` w.r.t. its original position

Torque acting on rod `tau = (dL)/(dt) = d/(dt)(Iomega) = omega (dI)/(dt)`
`=omega d/(dt)[112 MI^(2) + Mx^(2)] = 2M omega xx (dx)/(dt)`.......(i)
This torque is balanced by the torque due to weight of insect `tau`= Force `xx` Perpendicular distance of force with axis of rotation.
`=Mg xx (OM) = Mg xx x costheta`...........(ii)
From (i) and (ii)
`2Momega xx (dx)/(dt) = Mg xx x cos theta rArr dx =(g/(2omega)) cos omega tdt`
On integration taking limits
`int_(L//4)^(L//2) dx + g/(2omega^(2)) int_(0)^(pi//2omega) cos omega tdt` [when `x=L/4, omega t=0`, when `x=L/2 , omega t=pi/2`]
`[x]_(L//2)^(L//4) = g/(2omega^(2)) [sin omega t]_(0)^(pi//2omega)`
`rArr L/2 -L/4 =g/(2omega^(2))[sin pi/2 - sin 0] rArr L/4 =g/(2omega^(2)) rArr omega =sqrt((2g)/L)`
But `omega = 12/7 V/L rArr 12/7 V/L = sqrt((2g)/L) rArr V=7/12 sqrt(2gL) rArr V=7/12 sqrt(2 xx 10 xx 1.8) = 3.5 ms^(-1)`