Home
Class 12
PHYSICS
Consider two electric dipoles P(1) and ...

Consider two electric dipoles `P_(1)` and `P_(2)` placed at (0, 0) and (1,`sqrt2` ) respectively. The centers of these dipoles are fixed so that they can rotate about their centers but the centers cannot move. Answer the following questions based on this arrangement.

Initially `P_(1)` is held such that it is pointing towards positive x-axis and `P_(2)` is free to rotate. In the equilibrium position, `P_(2)` will point :

A

along x axis

B

along y-axis

C

along line joining `P_(1)` and `P_(2)`

D

along some arbitrary angle from x-axis

Text Solution

Verified by Experts

The correct Answer is:
B

In equilibrium position, `P_2` will align itself `botr to P_1` (along the electric field of `P_1`) along y-axis.
Promotional Banner

Similar Questions

Explore conceptually related problems

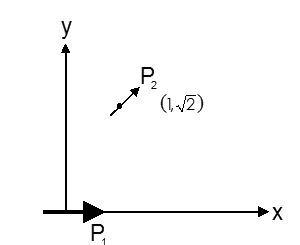
Consider two electric dipoles P_(1) and P_(2) placed at (0, 0) and (1, sqrt2 ) respectively. The centers of these dipoles are fixed so that they can rotate about their centers but the centers cannot move. Answer the following questions based on this arrangement. Now P_(2) is fixed in the equilibrium position obtained in last question and P_(1) is released so that it can rotate freely. In its equilibrium position P_(1) will point along:

Two short dipoles phat(k) and P/2 hat(k) are located at (0,0,0) & (1m, 0,2m) respectivley. The resultant electric field due to the two dipoles at the point (1m, 0,0) is

The electric field of an electric dipole at a point on its axis , at a distance d from the center of the dipole, varies as

Two point dipoles phat(k) and (P)/(2) hat(k) are located at (0, 0, 0) and (1m, 0, 2m) respectively. Find the resultant electric field due to the two dipoles at the point M(1m, 0, 0) [-((7P)/(32piin_(0)))hat(k)]

In the figure, two point charges +q and -q are placed on the x-axis at (+a,0) and (-a,0) respectively. A tiny dipole of dipolem moment (p) is kept at the origin along the y-axis. The torque on the dipole equals

An electric dipole of dipole moment P is lying along uniform electric field E. The work done in rotating the dipole by 37° is

Two point electric dipoles with dipole moment P_(1) and P_(2) are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=(1)/(4piepsilon_(0)) )