Home
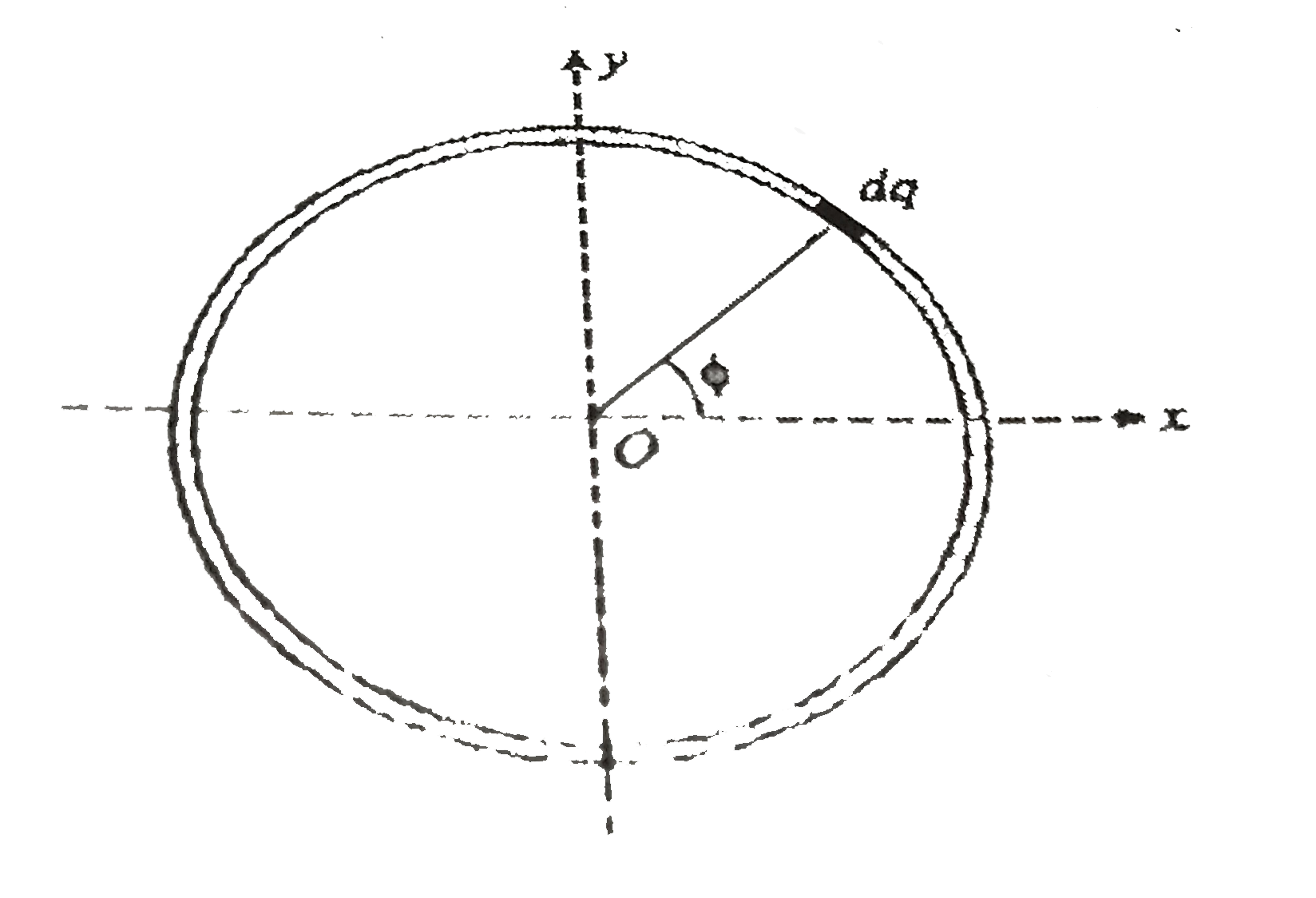
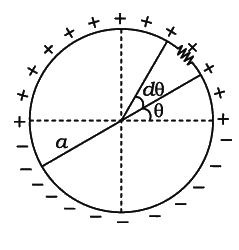
Class 12
PHYSICS
A thin non-conducting ring or radius a h...

A thin non-conducting ring or radius a has a linear charge density `lambda = lambda_(0) sin phi`. A uniform electric field `E_(0) hat(i) + E_(0) hat(j)` exist in the region . .Net torque acting on ring is given as :

A

`E_(0)sqrt2pia^(2)lamda_(0)`

B

`E_(0)pia^(2)lamda_(0)`

C

`2E_(0)pia^(2)lamda_(0)`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
D
`dq=(lamda_0 sin theta) ad theta`
`dp=dq times 2a=2a lamda_0 sin theta d theta`
Or `d overlinep=2a lamda_0 sin theta d theta [- cos theta hat i- sin theta hat j]`
Now `t= int_0 ^pi doverline p times overlineE`
`=2pi lamda_0 int_0^(pi) (- cos theta sin theta hat i -sin^2 theta hatj) ties (E_0 hatj +E_0 hat j)=E_0 pi a^2 lamda_0`
Promotional Banner

Similar Questions

Explore conceptually related problems

A thin non-conducting ring of radius R has a linear charge density lambda=lambda_(0) cos theta , where theta is measured as shown. The total electric dipole moment of the charge distribution is

A thin nonconducting ring of radius R has a linear charge density lambda = lambda_(0) cos varphi , where lambda_(0) is a constant , phi is the azimutahl angle. Find the magnitude of the electric field strength (a) at the centre of the ring , (b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x gt gt R .

A half ring of radius r has a linear charge density lambda .The potential at the centre of the half ring is

A cube of side a is placed in a uniform electric field E = E_(0) hat(i) + E_(0) hat(j) + E_(0) k . Total electric flux passing through the cube would be

A quarter ring of radius R is having uniform charge density lambda . Find the electric field and potential at the centre of the ring.

A uniform conducting ring of mass pi kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B = (hat (i) + t^(2) hat (j))T is present in the region, where t is time in seconds. Resistance of ring is 2 (Omega) . Then Induced electric field (in volt/meter) at the circumference of ring at the instant ring start toppling is