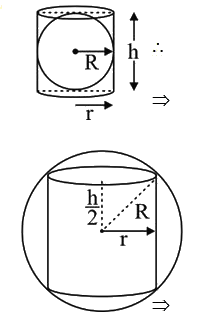
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A charged shell of radius R carries a total charge Q. Given phi as the...
Text Solution
|
- A charged shell of radius R carries a total charge Q. Given phi as the...
Text Solution
|
- a point charge q is placed at the centre of a cylinder of length L and...
Text Solution
|
- There is a hemispherical shell having charge Q uniformly distributed o...
Text Solution
|
- A conducting spherical shell having inner radius a and outer radius b ...
Text Solution
|
- A conducting shell of radius R carries charge -Q. A point charge +Q is...
Text Solution
|
- किसी लम्बे बेलनाकार कोश के ऊपरी भाग में धनात्मक पृष्ठ आवेश घनत्व sigma...
Text Solution
|
- A charge q is placed at the centre of a cylinder of radius R and lengt...
Text Solution
|
- A charge 'Q' is placed at the centre of a hemispherical surface of rad...
Text Solution
|