Four point charges `+8muC,-1muC,-1muC` and , `+8muC` are fixed at the points `-sqrt(27//2)m,-sqrt(3//2)m,+sqrt(3//2)m`
and `+sqrt(27//2)m` respectively on the y-axis. A particle of mass `6xx10^(-4)kg` and `+0.1muC` moves along the x-direction. Its speed at `x=+ infty` is `v_(0)`. find the least value of `v_(0)` for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.

Answer

`(v_(0) = 3m//s , x =3)`

Explanation

`(V_(0) = 3m // s, x = 3)`

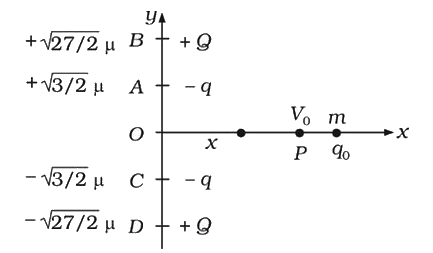
In the figure ` q = 1 mu C = 10^(-6) C , q_(0) = + 0.1 mu C = 10^(-7) C ` and ` m = 6 xx 10^(-4) Kg ` and Q ` = 8 mu C`
Let P be any point at a distance x from origin O . Then
`AP = CP = sqrt((3)/(2)+X^(2))`
` BP = DP=sqrt((27)/(2) + x^(2))`
Electric potential at point P will be, `V = (2KQ)/(BP) - (2kq)/(AP)`
Where `K = (1)/(4 pi epsi_(0)) = 9 xx 10^(9) N m//C^(2)`
`therefore " " V = 2 xx 9 xx 10^(9) [(8 xx 10^(-6))/(sqrt((27)/(2))+ x^(2)) + sqrt((3)/(2)+x^(2))] , v = 1.8 xx 10^(4) [ (8)/(sqrt((27)/(2)+x)) - (1)/(sqrt((3)/(2)+x^(2))]`
Electric field at P
`E = -(dV)/(dx) = 1.8 xx 10^(4) [ (beta) ((-1)/(2)) ((27)/(2) + x^(2))^(-3//2) (-(1)/(2)) ((3)/(2) + x^(2))^(-3//2)](2x)`
E = 0 on x-axis where x = 0 or `(8)/((27)/(2) + x^(2))^(3//2) = (1)/((3)/(2)+x^(2))^(3//2)`
`rArr ((4)^(3//2))/((27)/(2) + x^(2))^(3//2) = (1)/((3)/(2))+ x^(2))^(3//2) rArr ((27)/(2) + x^(2)) = 4((3)/(2)+ x^(2))`
This equation gives ` x = pm sqrt((5)/(2)) m`
The least value of kinetic energy of the particle at infinity should be enough to take the particle upto ` x = pm sqrt((5)/(2))` m because at ` x = + sqrt((5)/(2))m , E= 0` . `rArr` Electrostatic force on charge q is zero or `F_(e) = 0 `
For at `x gt sqrt((5)/(2))m` E is repulsive ( towards positive x - axis) & for ` x gt sqrt((5)/(m))`, E is attractive (towards negative x axis). Now form Eq (i) potential at `x = sqrt((5)/(2))m`.
`V = 1.8xx 10^(4) [(8)/(sqrt((27)/(2) + (5)/(2)))-(1)/(sqrt((3)/(2) + (5)/(2)))] , v_(0) = sqrt((2q_(0)V)/(m))`
Substituting the value
`V_(0) = sqrt((2 xx 10^(-7) xx 2.7xx 10^(4))/(6 xx 10 ^(-4))) rArr v_(0) = 3 m//s therefore `Minimum value of `v_(0)` is `3m//s`
From Eq (i) , potential orgin ( x = 0) is , ` v_(0) = 1.8xx 10^(4) [(8)/(sqrt(27)/(2)) - (1)/(sqrt((3)/(2))] = 2.4xx 10^(4)V`
Let be the kinetic energy of the particle at origin. Applying energy conservation at and at `k + q_(0) v_(0) = (1)/(2)m v_(0)^(2)`
But `(1)/(2) m v_(0)^(2) = q_(0) V` [ form Eq (i)]
` k = q_(0) (V - V_(0))` ,
` k =(10^(-7)) (2.7 xx 10^(-4) - 2.4 xx 10^(4))` , ` k = 3 xx 10^(-4) J`