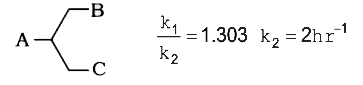Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- An organic compound (A) decomposes according to two parallel first ord...
Text Solution
|
- Conisder a mechanism in which a single reactant profuces several Produ...
Text Solution
|
- If the dissociation constants of two substances are K(1) " and " K(2) ...
Text Solution
|
- A substance undergoes first order decomposition. The decomposition fol...
Text Solution
|
- An organic compound (A) decomposes according to two parallel first ord...
Text Solution
|
- The substance undergoes first order decomposition. The decomposition f...
Text Solution
|
- k(1)=xhr^(-1), k(1): k(2) =1:10 . Calculate ([C])/([A]) after one hour...
Text Solution
|
- समान अभिक्रिया परिस्थितियों में, एक पदार्थ की प्रारम्भिक सान्द्रता, 1....
Text Solution
|
- Under the same reaction condition the initial concentration of 1.386 m...
Text Solution
|
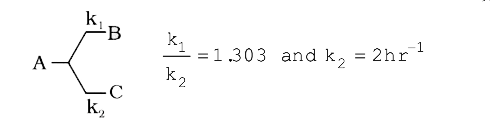 `(k_(1))/(k_(2))=1.303 and k_(2) =2hr^(-1)`
`(k_(1))/(k_(2))=1.303 and k_(2) =2hr^(-1)`