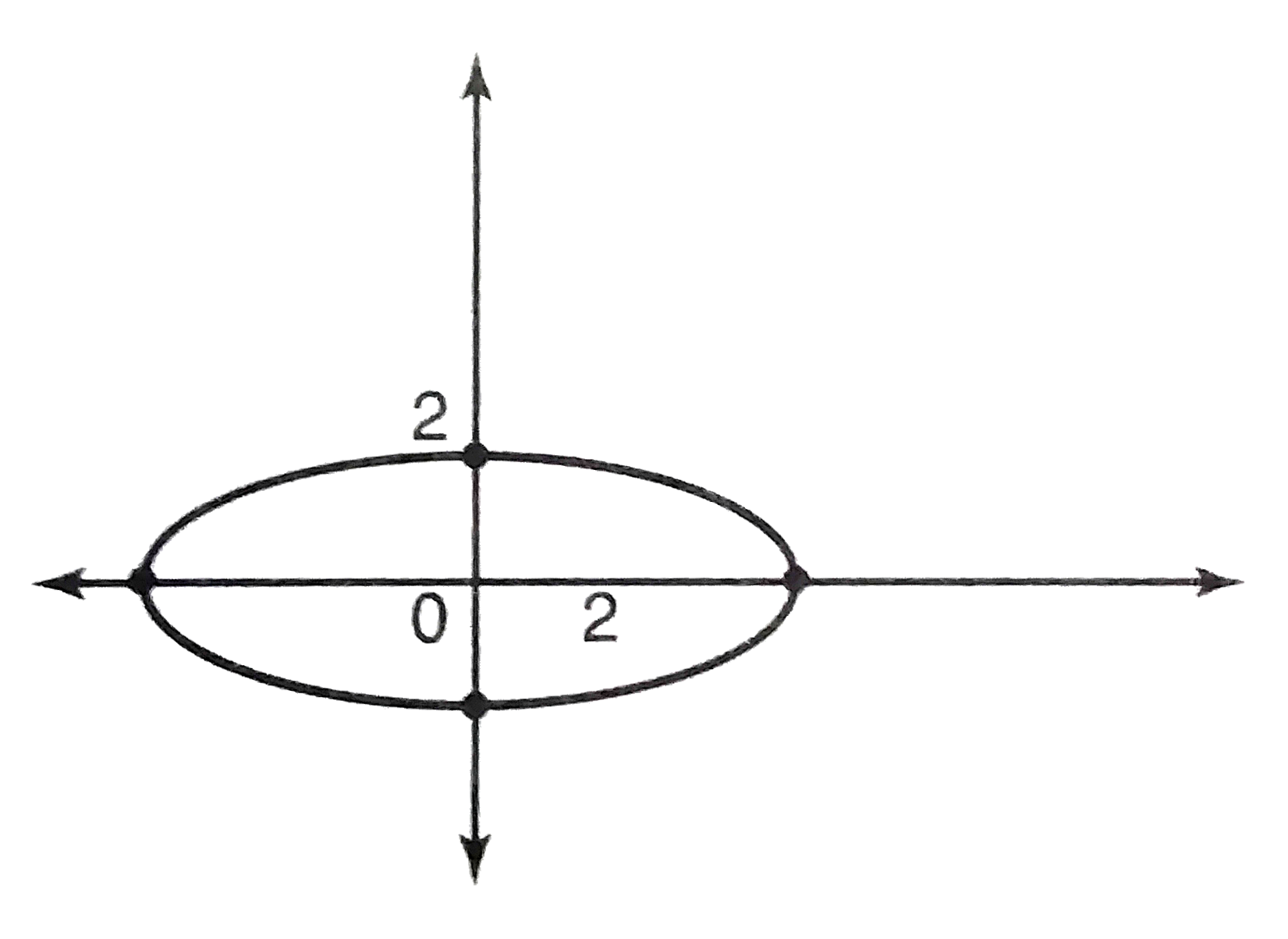
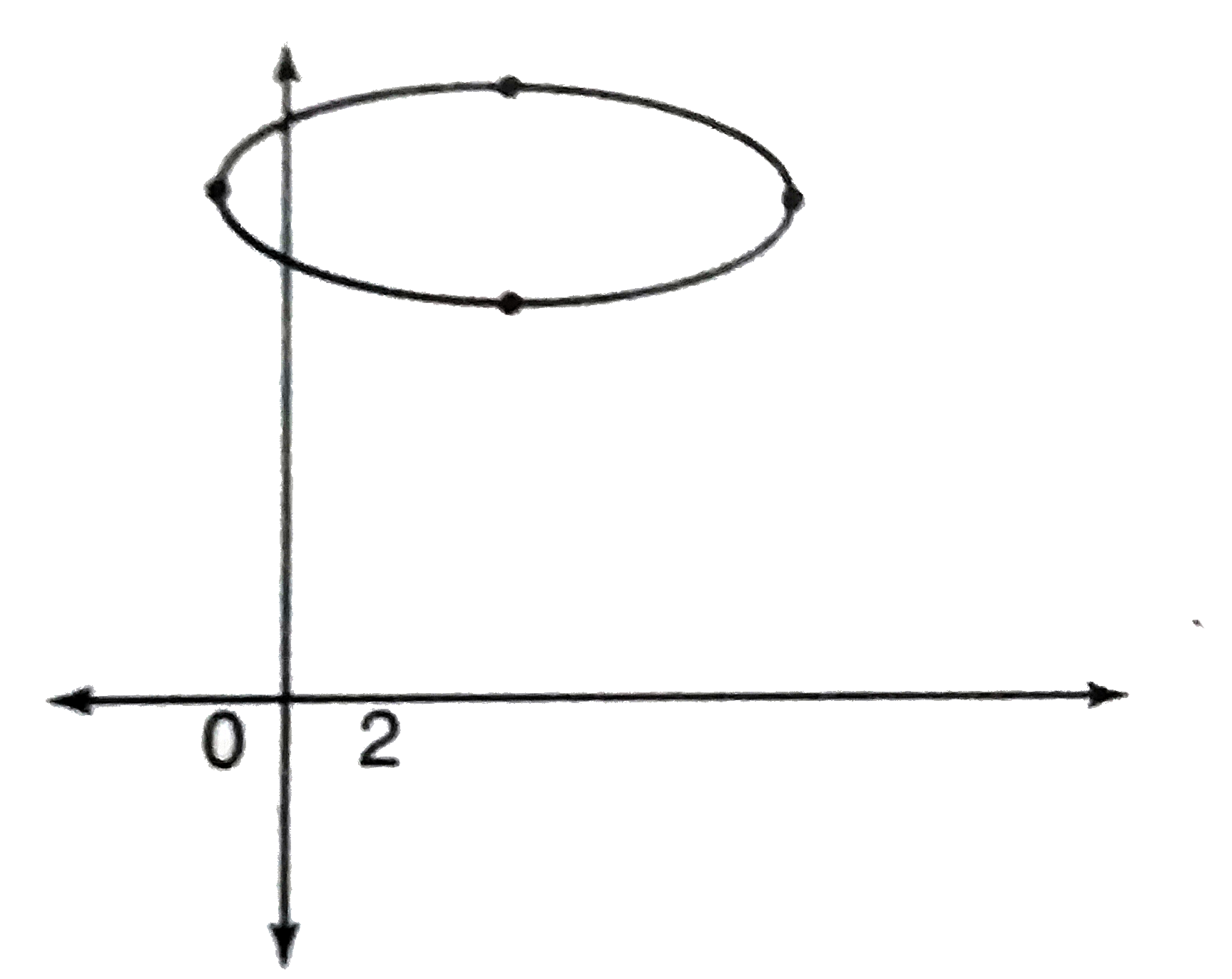
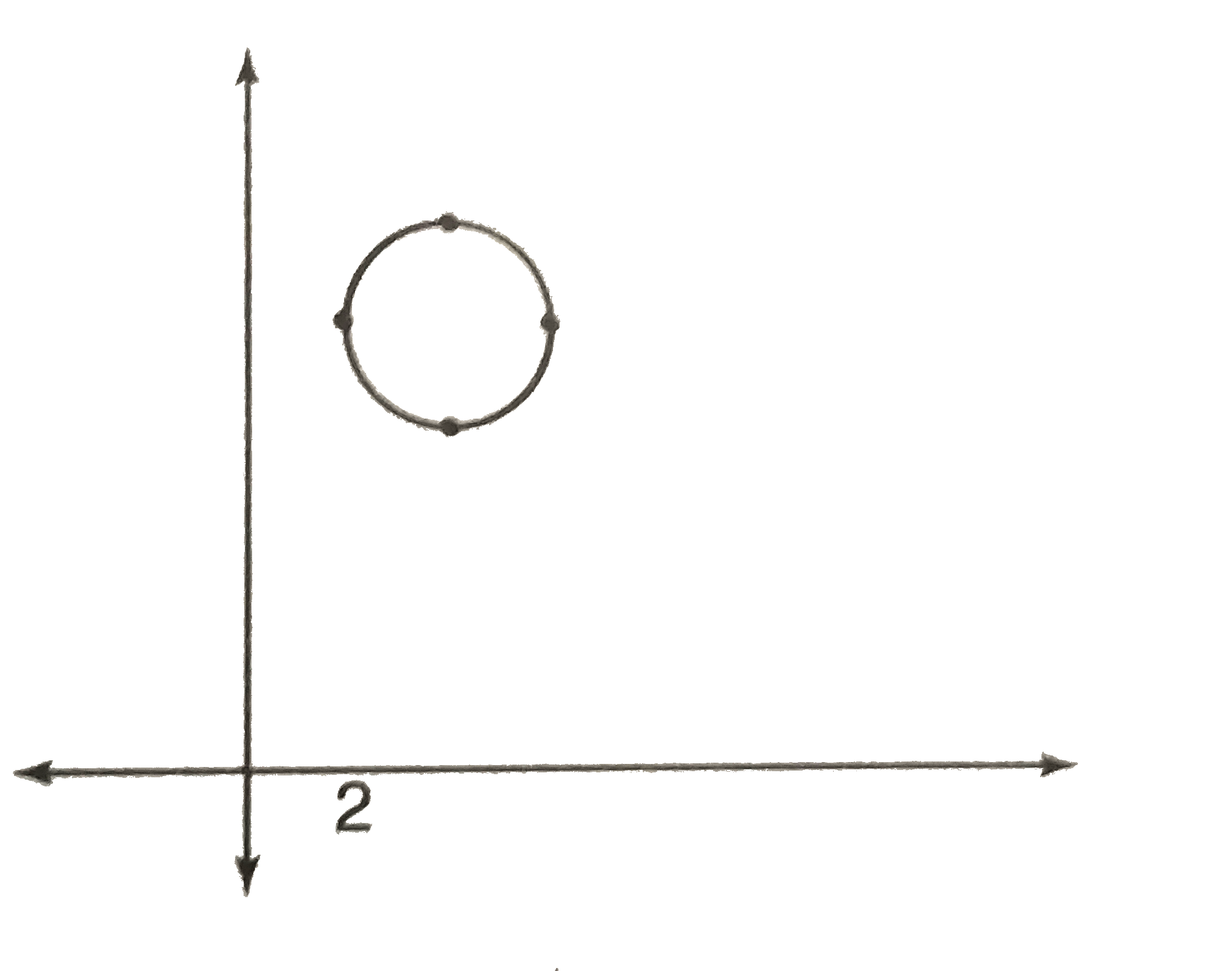
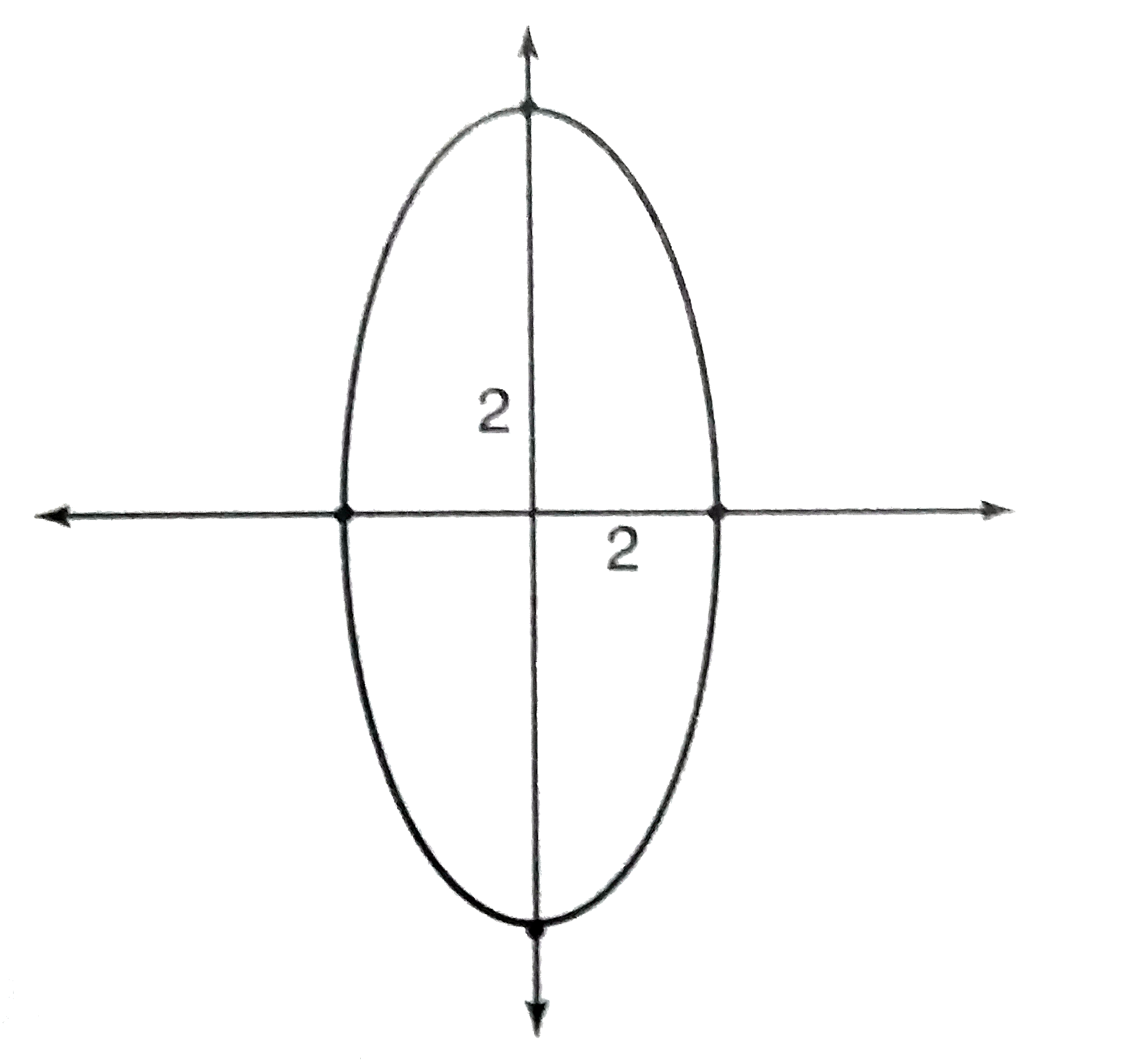
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Select the graph of ((x-4)^2)/(25)+((y-9)^2)/4=1
Text Solution
|
- Suppose x,y in(-2,2) and xy=-1 then the minimum value of a=(4)/(4-x^(2...
Text Solution
|
- The equation of the ellipse whose vertices are (9,2),(-1,2) and the di...
Text Solution
|
- Factorize each of the following expressions: (1)x^4-625 (2) x^4-1 ...
Text Solution
|
- From the graph of y=x^(2)-4, draw the graph of y=(1)/(x^(2)-4).
Text Solution
|
- Find the (i)length of the axis(ii)coordinate of vertices (iii)coordina...
Text Solution
|
- Factorise : ((25)/(4)x^2-(1)/(9)y^2)
Text Solution
|
- गुणनखण्ड ज्ञात कीजिए : (25)/(4)x^(2)-(y^(2))/(9)
Text Solution
|
- The minimum length of intercept on any tangent to the ellipse (x^(2))/...
Text Solution
|