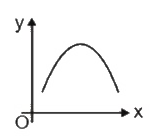
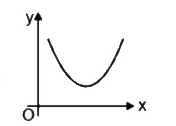
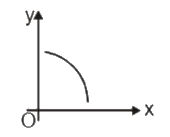
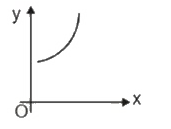
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If slope of curve is first positive, then zero and after that became n...
Text Solution
|
- Can position-time graph have negative slope ?
Text Solution
|
- What do the slopes of distance-time and velocity-time graphs represen...
Text Solution
|
- Which of the following graphs represents the position time-graph of a ...
Text Solution
|
- The above curve shows the graph of a^(x) under which one of the follow...
Text Solution
|
- STATEMENT - 1 : All accelerated object are represented on position-tim...
Text Solution
|
- निम्न ग्राफों का ढलान क्या प्रदर्शित करता है? (i)स्थिति-समय ग्राफ, (...
Text Solution
|
- In the above graph, which slope represents more species richness ?
Text Solution
|
- If slope of curve is first positive, then zero and after that became n...
Text Solution
|