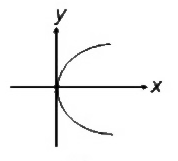
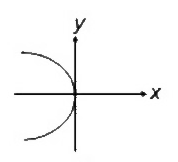
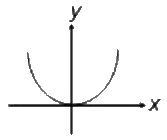
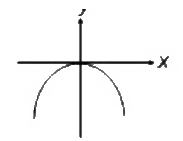
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which of the following can represent the curve x^(2) = -2y ?
Text Solution
|
- Form the differential equation representing the family of curves give...
Text Solution
|
- Which of the following are true for the curve represented by the diffe...
Text Solution
|
- Which of the following may represent the curve x = 2y+ 3?
Text Solution
|
- Which of the following can represent the curve x^(2) = -2y ?
Text Solution
|
- Form the differential equation representing the family of curves given...
Text Solution
|
- Form the differential equation representing the family of curves give...
Text Solution
|
- Form the differential equation representing the family of curves give...
Text Solution
|
- Form the differential equation representing the family of curves give...
Text Solution
|