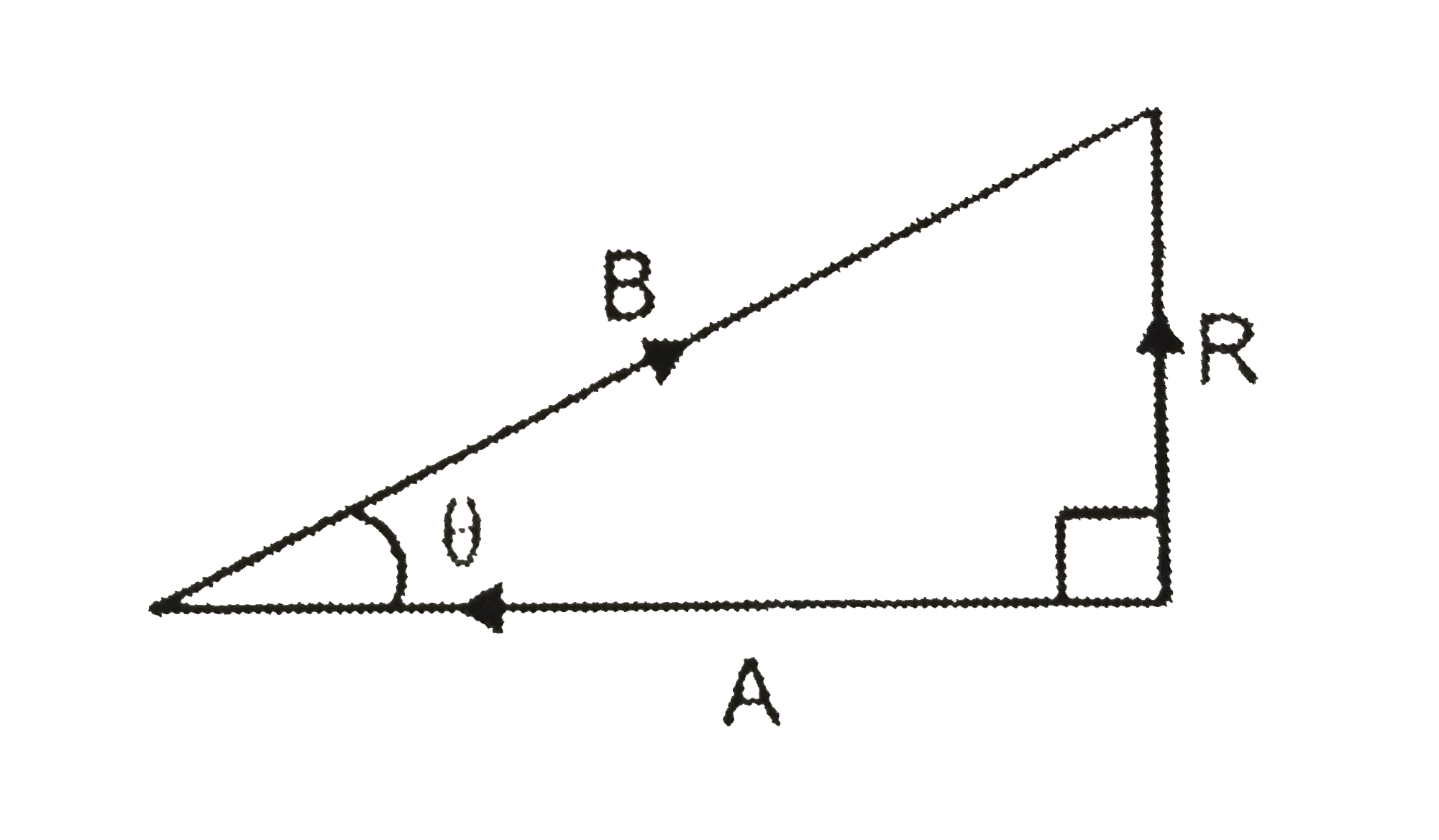
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In vector diagram shown in figure where (vecR) is the resultant of vec...
Text Solution
|
- In vector diagram shown in figure where (vecR) is the resultant of vec...
Text Solution
|
- Let vecr be a unit vector satisfying vecr xx veca = vecb, " where " |v...
Text Solution
|
- In vector diagram shown in figure where (vecR) is the resultant of vec...
Text Solution
|
- निम्नांकित चित्र (a) में किसी कोण theta पर झुके हुए दो वेक्टर vecA तथ...
Text Solution
|
- Two vectors vecA and vecB inclined at an angle theta have a resultant ...
Text Solution
|
- चित्र में दिखाये गये दो सदिशों vecA और vecB के बीच का कोण theta है। इन...
Text Solution
|
- The vecR is in Figure 2.89 vecA Oh vecB The gain of two vectors. R=B/s...
Text Solution
|
- vecR is the resultant of the vectors vecA and vecB. If R=B/(sqrt(2)) t...
Text Solution
|