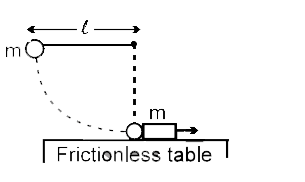
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The bob of a simple pendulum of length l dropped from a horizontal pos...
Text Solution
|
- A simple pendulum of length l has maximum angular displacement theta ....
Text Solution
|
- A simple pendulum bob has a mass ''m'' and length ''L'' . The bob is d...
Text Solution
|
- The bob of a simple pendulum (mass m and length l ) dropped from a hor...
Text Solution
|
- A simple pendulum of length l has a maximum angular displacement theta...
Text Solution
|
- लम्बाई l के सरल लोलक को क्षैतिज स्थिति से छोड़ने पर दोलन करते समय उसके ...
Text Solution
|
- A simple pendulum is released from A as shown. If m and 1 represent th...
Text Solution
|
- If a simple pendulum of length 'L' has maximum angular displacement al...
Text Solution
|
- The bob of a simple pendulum of length l dropped from a horizontal pos...
Text Solution
|