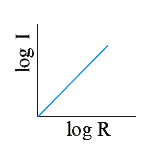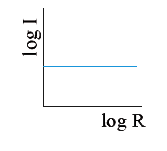A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
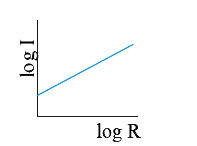
- In the above question, the curve between log I and log R will be :
Text Solution
|
- The area bounded by the curves y=ln x,y=ln|x|,y=|ln x| and y=|ln||x| i...
Text Solution
|
- Sketch the curve y="log"|x|
Text Solution
|
- log(log i)=
Text Solution
|
- If l^(r)(x) means log log log...x,the log being repeated r xx,then int...
Text Solution
|
- The area between the curves y=ln x and y=(ln x)^(2) is
Text Solution
|
- The graph between log R and log A wher R is the nuclear radius and A i...
Text Solution
|
- If p^(th), q^(th), r^(th) terms of a geometric progression are the pos...
Text Solution
|
- In the above question, the curve between log I and log R will be :
Text Solution
|