Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
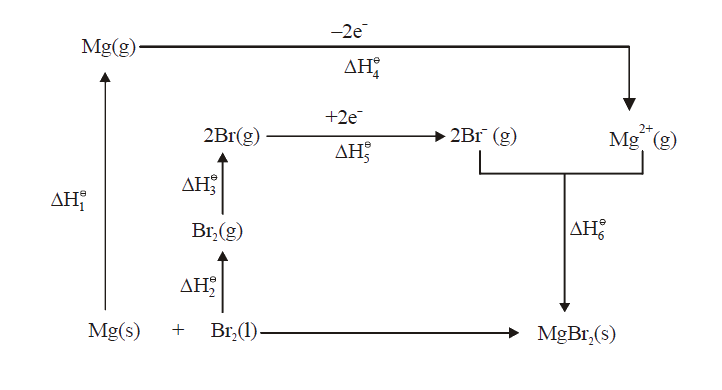
- Calculate the lattice enthalpy of MgBr(2) from the given date: {:(M...
Text Solution
|
- Find DeltaH of the process NaOH(s) rarr NaOH(g) Given: Delta(diss)H^(T...
Text Solution
|
- Calculate the lattice enthalpy of MgBr(2) from the given date: {:(Mg(s...
Text Solution
|
- on the basis of thermochemical equation a,b and c, find out which of t...
Text Solution
|
- The Delta(f) H^(@) (N(2)O(5), g) in kJ/mol on the basic of the followi...
Text Solution
|
- Three thermochemical equations are given below (1) C(("graphite"))+O(2...
Text Solution
|
- Given C(("graphite"))+O(2)(g)rarrCO(2)(g), " "Delta(r)H^(@)=-393.5 kJ ...
Text Solution
|
- Calculate the enthalpy change for the process C Cl(4)(g) rarr C(g)+4...
Text Solution
|
- Given C(("graphite"))+O(2)(g)toCO(2)(g), Delta(r)H^(0)=-393.5kJ" "mo...
Text Solution
|