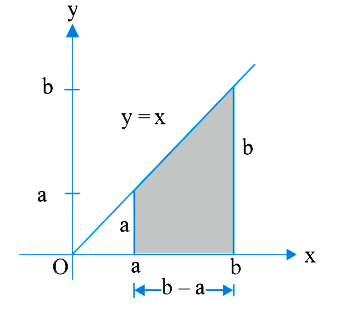
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Using the concept of integration evaluate an area by definite integral
Text Solution
|
- Area as a definite integral
Text Solution
|
- Using definite integration,find the area of the smaller region bounded...
Text Solution
|
- Evaluate the following integrals using the definition of definite inte...
Text Solution
|
- Evaluate the following integrals using the definition of definite inte...
Text Solution
|
- Using the concept of integration evaluate an area by definite integral
Text Solution
|
- By using the properties of definite integrals, evaluate the integrals ...
Text Solution
|
- Definite Integration|Properties of Definite integration#!#Question Bas...
Text Solution
|
- Evaluate the following integrals using the definition of a definite in...
Text Solution
|