Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
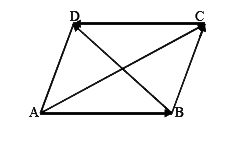
- Figure shows a parallelogram ABCD. Prove that vec(AC)+ vec (BD) = 2 ve...
Text Solution
|
- Let ABCD is a parallelogram and vecAC, vecBD be its diagonal, then vec...
Text Solution
|
- In the parallelogram ABCD,vec AC^(2)-vec BD^(2)=
Text Solution
|
- ABCD is a parallelogram Fig. 2 (c ) .64. AC and (BD) are its diagonals...
Text Solution
|
- A parallelogram ABCD. Prove that vec(AC)+ vec (BD) = 2 vec(BC)'
Text Solution
|
- If ABCD is a parallelogram, then vec(AC) - vec(BD) =
Text Solution
|
- ABCD एक समांतर चतुर्भुज है ।AC और BD इसके विकर्ण है । सिद्ध कीजिए - ...
Text Solution
|
- समान्तर चतुर्भुज ABCD में, माना vec(AB) = vec(a) और vec(BC) = vec(b), ...
Text Solution
|
- ABCD एक समान्तर चतुर्भुज हैं और AC, BD इसके विकर्ण हैं| (a) vec(AB) ...
Text Solution
|