A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THERMODYNAMICS
NCERT EXEMPLAR|Exercise VERY SHORT ANSWER TYPE QUESTIONS|5 VideosTHERMODYNAMICS
NCERT EXEMPLAR|Exercise SHORT ANSWER TYPE QUESTIONS|6 VideosTHERMODYNAMICS
NCERT EXEMPLAR|Exercise LONG ANSWER TYPE QUESTIONS|5 VideosTHERMAL PROPERTIES OF MATTER
NCERT EXEMPLAR|Exercise Very short Answer type Questions|15 VideosUNITS AND MEASUREMENTS
NCERT EXEMPLAR|Exercise Long Answer Type Questions|9 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-THERMODYNAMICS -MULTIPLE CHOICE QUESTIONS (MORE THAN ONE OPTIONS)
- Which of the processes described below are irreversible ?
Text Solution
|
- An idel gas undrgoes isothermal process from some initial state i to f...
Text Solution
|
- Figure shows the p-V diagram of an ideal gas undergoing a change of st...
Text Solution
|
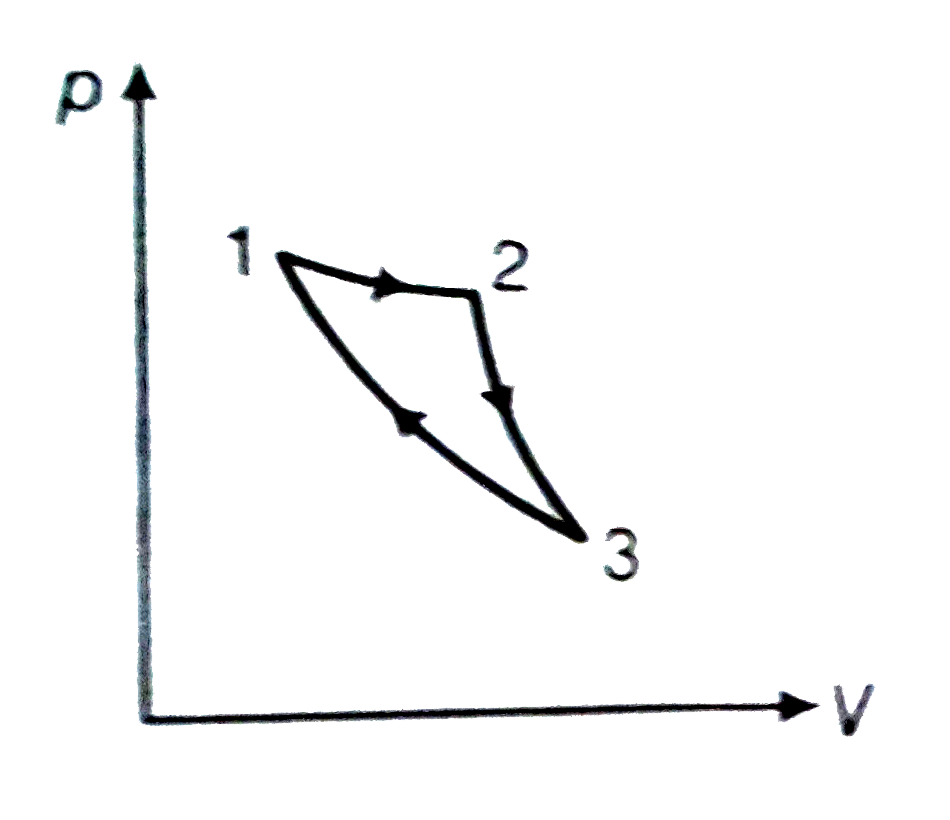
- Consider a cycle followed by an engine (figure.) 1 or 2 is isoth...
Text Solution
|
- Consider a heat engine as shown in figure. Q(1)and Q(2) are heat added...
Text Solution
|