Text Solution
Verified by Experts
Recommended Questions
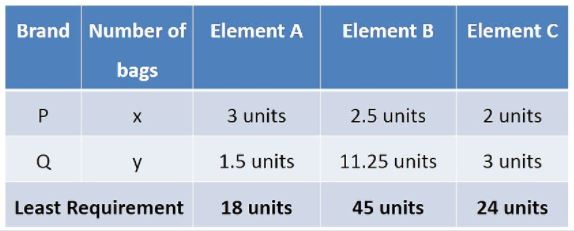
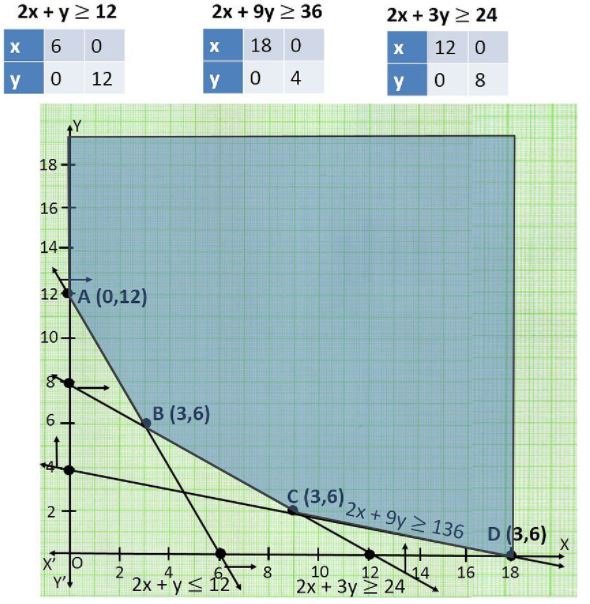
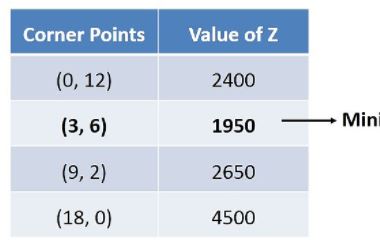
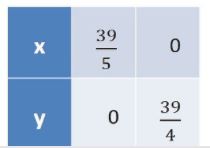
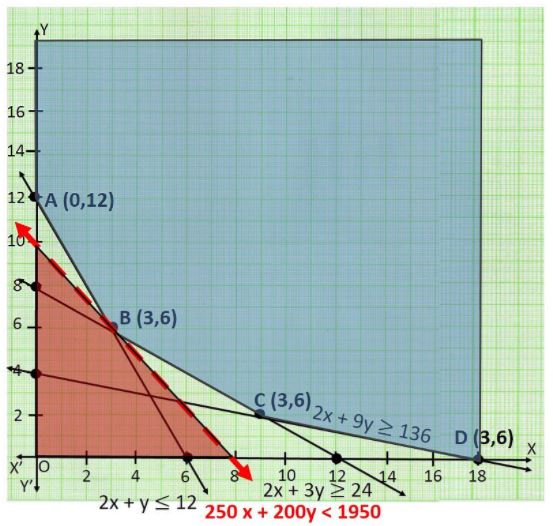
- A farmer mixes two brands P and Q of cattle feed. Brand P, costing ...
Text Solution
|
- Reshma wishes to mix two types of food P and Q in such a way that the...
Text Solution
|
- A farmer mixes two brands P and Q of cattle feed. Brand P, costing ...
Text Solution
|
- Reshma wishes to mix two types of food P and Q in such a way that the ...
Text Solution
|
- A farmer mixes two brands P and Q of cattle feed. Brand P costing Rs. ...
Text Solution
|
- एक किसान दो प्रकार के चारे P और Q को मिलाता (मिश्रण ) है । P प्रकार के...
Text Solution
|
- एक किसान दो प्रकार के चारे P और Q को मिलता (मिश्रण) है । P प्रकार के च...
Text Solution
|
- एक किसान दो प्रकार के चारे P और Q को मिलता ( मिश्रण ) है । P प्रकार के...
Text Solution
|
- एक बीमार व्यक्ति के लिए एक आहार से कम-से-कम विटामिन की 4000 इकाइयां , ...
Text Solution
|