A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-SETS-OBJECTIVE TYPE QUESTIONS
- Suppose, A(1),A(2),"……..",A(30) are thirty sets each having 5 element...
Text Solution
|
- Two finite sets have m and n elements. The number of subsets of the...
Text Solution
|
- The set (AuuB^(prime))^'uu(BnnC) is equal to A 'uuBuuC b. A 'uuB c. A ...
Text Solution
|
- Let F(1) be the set of parallelograms, F(2) the set of rectangle , F(...
Text Solution
|
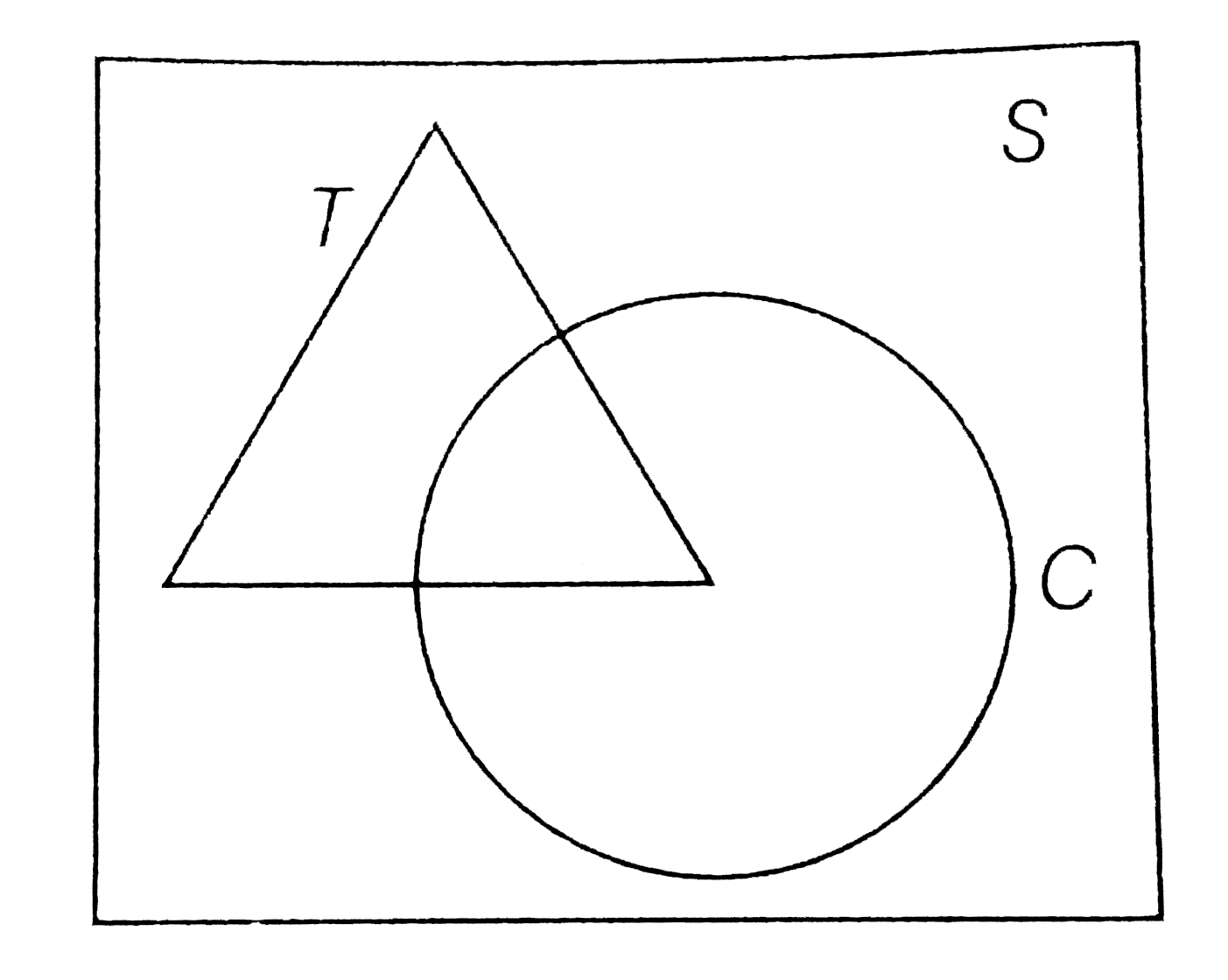
- Let S= set of point inside the square, T= set of points inside the tri...
Text Solution
|
- Let R be set of points inside a rectangle of sides a and b (a, b > 1) ...
Text Solution
|
- In a town of 840 persons , 450 persons read Hindi, 300 read English an...
Text Solution
|
- If X={8^n-7n-1 | n in N} and Y={49n-49| n in N}. Then
Text Solution
|
- A survey shows that 63% of the people watch a news channel whereas ...
Text Solution
|
- If set A and B are defined as A = {(x,y)|y = 1/x, 0 ne x in R},...
Text Solution
|
- If A and B are two sets A nn(A uu B)=
Text Solution
|
- If A={1,3,5,7,9,11,13,15,17}, B={2,4,.......,18} and N the set of natu...
Text Solution
|
- If S = {x:x is a positive multiple of 3 less than 100} and P = {x ...
Text Solution
|
- If A and B are two sets, then A nn (A uu B)' is equal to -
Text Solution
|