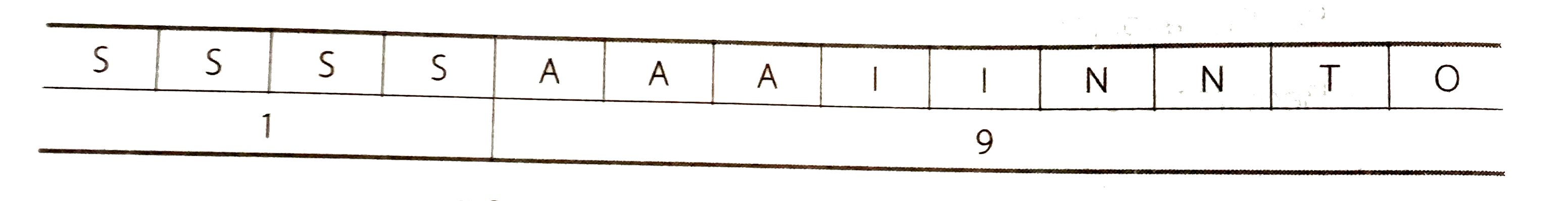Text Solution
Verified by Experts
Topper's Solved these Questions
PROBABILITY
NCERT EXEMPLAR|Exercise Objective Type Questions|12 VideosPROBABILITY
NCERT EXEMPLAR|Exercise True/False|7 VideosPROBABILITY
NCERT EXEMPLAR|Exercise Matching The Columns|2 VideosPRINCIPLE OF MATHEMATICAL INDUCTION
NCERT EXEMPLAR|Exercise OBJECTIVE TYPE QUESTIONS|5 VideosRELATIONS AND FUNCTIONS
NCERT EXEMPLAR|Exercise True /False|5 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-PROBABILITY-Long Answer Type Questions
- One urn contains two black balls (labelled B1 and B2) and one white ...
Text Solution
|
- A bag contain 8 red and 5 white balls. Three balls are drawn at random...
Text Solution
|
- If the letters of the word ASSASSINTION are arranged at random. Find ...
Text Solution
|
- A card is drawn from a deck of 52 cards. Find the probability of ge...
Text Solution
|
- A sample space consists of 9 elementary outcomes E(1),E(2),…..,E(9) wh...
Text Solution
|
- Determine the probability p, for each of the following events. (i) A...
Text Solution
|