Here, `5=2^(2)+1^(2)`
So, draw a right angled `DeltaOAB`in which OA= 3 units and AB =1 units and `angleOAB=90^(@)` By using pythagoras theorem, we get
`OB=sqrt(OA^(2)+AB^(2))`
`sqrt(2^(2)+1^(2))=sqrt(4+1)=sqrt5`
Taking `OB=sqrt5` as radius and point ) as centre, draw an arc which meets the number line at point P on the postive, side of it.
Hence, it is clear that point P represent `sqrt5` on the number line.

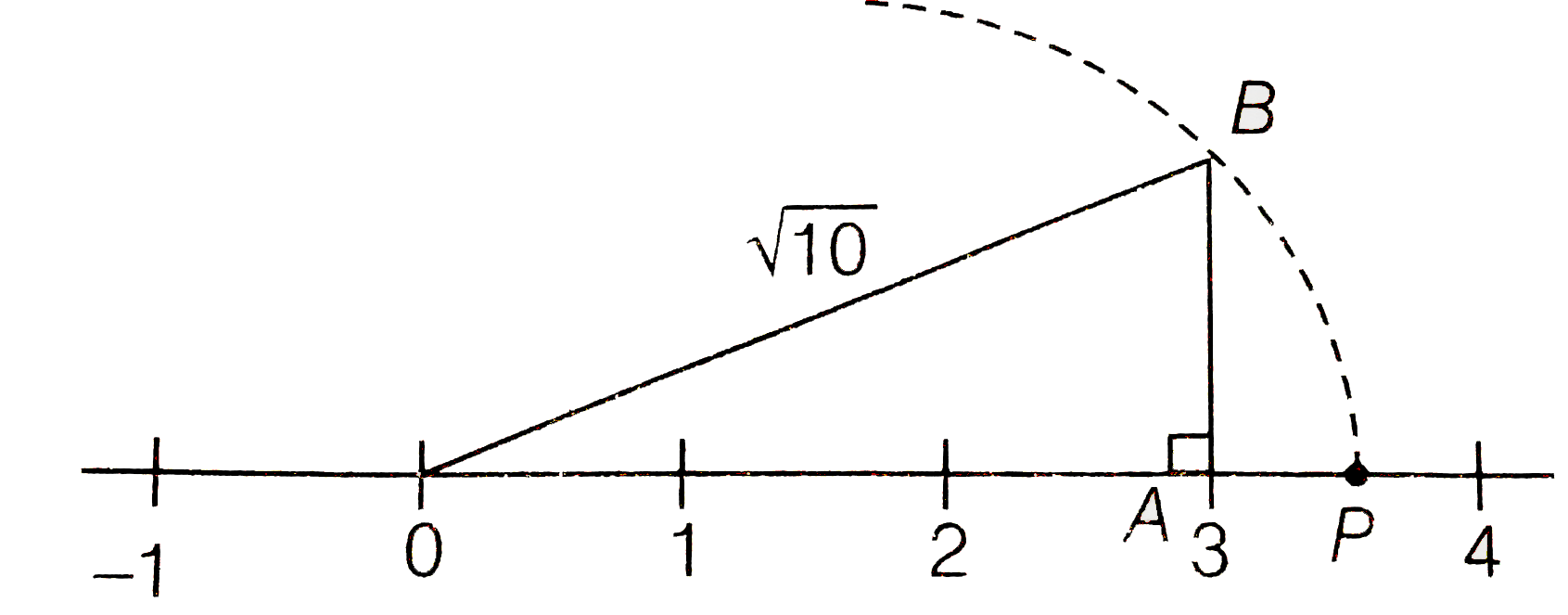
(ii) Here, `10 = 3^(2)+1`
So, draw a right angled `DeltaOAB` in which OA=3 units and AB=1 units and `angleOAB=90^(@)`
By using Pythagoras theorem, we get
` OB= sqrt(OA^(2)+AB^(2))`
`sqrt(3^(2)+1^(2)) = sqrt(9+1)= sqrt10`
Taking `OB=sqrt10` radius and point O as centre, draw an arc which meets the number line at point p on the positive of it. the point P represents `sqrt10` on the number line.
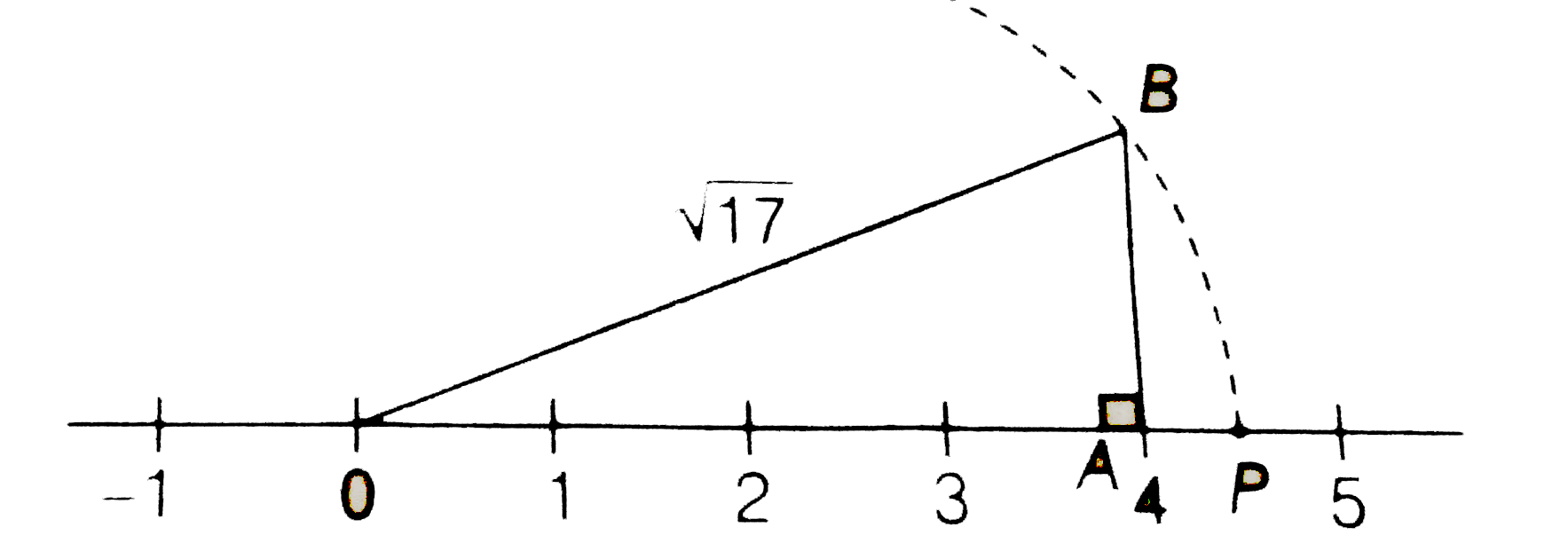
(iii) Here, `17=4^(2)+1`
So, draw a right angled `DeltaOAB`, in which OA=4 units and AB=1 unit and `angleOAB=90^(@)` by using Pythagoras theorem, we get
`OB=sqrt(OA^(2)+AB^(2)`
`=sqrt(4^(2)+1^(2))= sqrt(16+1)=sqrt17`
Taking `OB=sqrt17` as radius and point O as centre, draw arc which meets the number line at point P on the postive side of it. the point P respesents `sqrt` on the number line.