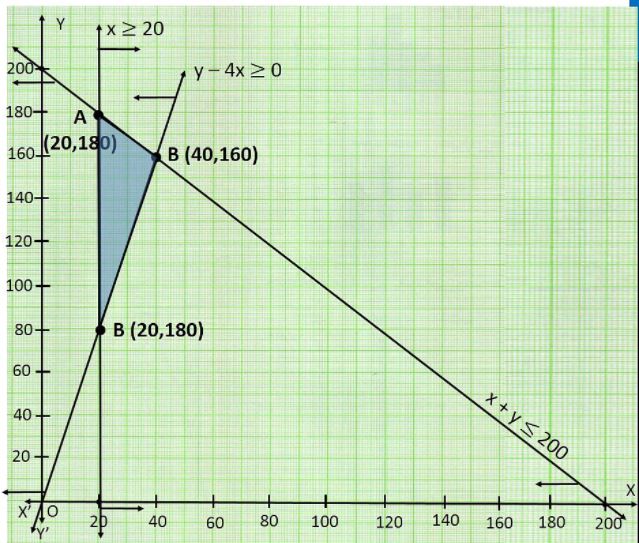
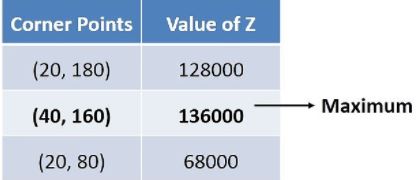
Text Solution
Verified by Experts
Recommended Questions
- An aeroplane can carry a maximum of 200 passengers. A profit of Rs 10...
Text Solution
|
- An aeroplane can carry a maximum of 200 passengers. A profit of Rs 10...
Text Solution
|
- An aeroplane can carry a maximum of 200 passengers. A profit of Rs....
Text Solution
|
- An aeroplane can carry a maximum of 200 passengers. A profit of Rs....
Text Solution
|
- An aeroplane can carry a maximum of two passengers. A profit of Rs. 10...
Text Solution
|
- एक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है । प्रत्येक प्र...
Text Solution
|
- एक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है। प्रत्येक प्रथ...
Text Solution
|
- एक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है । प्रत्येक प्र...
Text Solution
|
- एक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है। प्रत्येक प्रथ...
Text Solution
|