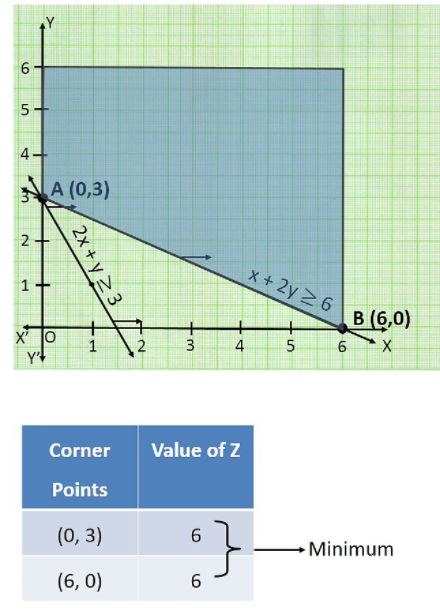
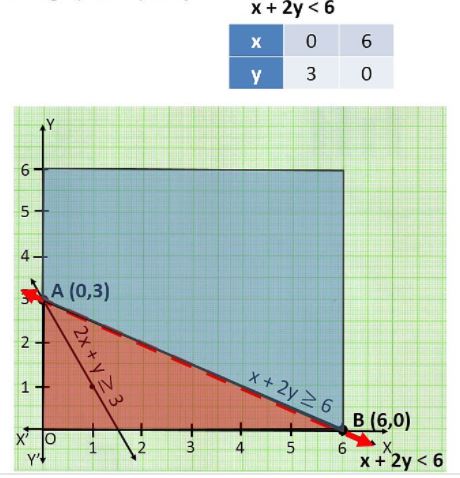
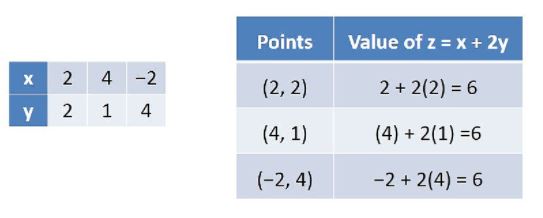
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Solve the following Linear Programming Problem graphically : Minimis...
Text Solution
|
- Solve the Following Linear Programming Problem graphically : Maximise...
Text Solution
|
- Solve the following Linear Programming Problem graphically : Minimis...
Text Solution
|
- Solve the Following Linear Programming Problem graphically : Minimise...
Text Solution
|
- Solve the following linear programming problem graphically :Minimise ...
Text Solution
|
- Solve each of the following linear programming problems by graphical ...
Text Solution
|
- Solve the Following Linear Programming Problem graphically : Maximise...
Text Solution
|
- Solve the Following Linear Programming Problem graphically : Minimise...
Text Solution
|
- Solve the Following Linear Programming Problem graphically : Maximise...
Text Solution
|