Home
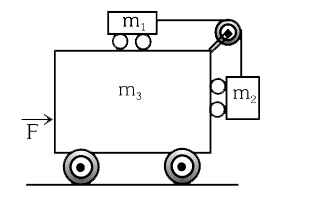
Class 12
PHYSICS
All surfaces assumed to be frictionless ...

All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that `m_(1)` and `m_(2)` do not move relative to `m_(3)` is :–

A

`(m_(1)+m_(2)+m_(3))(m_(2)g)/(m_(1))`

B

`(m_(1)+m_(2))(m_(2)g)/(m_(1))`

C

`(m_(2)+m_(3))(m_(1)g)/(m_(2))`

D

`(m_(1)+m_(3))(m_(1)g)/(m_(2))`

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • NEWTON'S LAWS OF MOTION & FRICTION

    MOTION|Exercise Exercise - 2 SECTION-C :- Pseudo force, Weighing Machine|2 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    MOTION|Exercise Exercise - 2 SECTION-D :- Spring force and spring cutting problems|1 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    MOTION|Exercise Exercise - 2 SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems|23 Videos

  • MODERN PHYSICS -1

    MOTION|Exercise EXERCISE-4 ( LEVEL- II)|39 Videos

  • NLM & FRICTION

    MOTION|Exercise EXERCISE-4 ( LEVEL-II)|15 Videos

Similar Questions

Explore conceptually related problems

What force F must be applied so that m_(1) and m_(2) are at rest on m_(3) in

A large cubical shaped block of mass M rests on a fixed horizontal surface. Two blocks of mass m_(1) and m_(2) are connected by a light inextensible string passing over a light pulley as shown. Neglect friction everywhere. Then the constant horizontal force of magnitude F that should be applied to M so that m_(1) and m_(2) do not mov relative to M is:

In the figure2.217 all the surfaces are frictionless. What force F is required to be applied on the bigger block so that m_(2) and m_(3) will remain at rest on it.

Two blocks of mass m_(1) = 6 kg and m_(2) = 3kg are as shown in the diagram. Coefficient of friction between m_(1) and m_(2) and between m_(1) and m_(2) and between m_(1) and the surface is 0.5 and 0.4 , respectively . The maximum horizontal force that can be applied to the mass m_(1) so that they move without separation is

For the system shown in fig, there is no friction anywhere. Masses m_(1) and m_(2) can move up or down in the slots cut in mass M. Two non-zero horizontal force F_(1) and F_(2) are applied as shown. The pulleys are massles and frictionless. Given m_(1) != m_(2) Let F_(1) and F_(2) are applied in such a way that m_(1) and m_(2) do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m_(1) gt m_(2) .

In the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is mu=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

A wedge of mass M makes an angle theta with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?

A block of mass 100 kg is set into motion on a frictionless horizontal surface with the help of a frictionless pulley and rope system shown in What horizontal force should be applied on the rope to produce an acceleration of 0.1 m//s^(2) .

In the adjoining figure all surface are frictionless . What force F must by applied to M_(1) to keep M_(3) free from rising or falling?