Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS-Introduction To Trigonometry And Its Applications
- An observer, 1.5 m tall, is 20.5 m away from a tower 22 m high. Determ...
Text Solution
|
- Prove the following identity: sec^4theta-sec^2theta=tan^4theta+tan^2th...
Text Solution
|
- If cosectheta + cottheta=p, then cos theta=
Text Solution
|
- Prove that sqrt(sec^(2)theta + cosec^(2)theta) = tantheta + cottheta.
Text Solution
|
- The angle of elevation of the top of a tower from a certain point is 3...
Text Solution
|
- If 1+sin^(2)theta = 3sinthetacostheta, then prove that tantheta=1 or 1...
Text Solution
|
- If sintheta + 2 costheta=1,then 2sintheta-costheta=
Text Solution
|
- The angle of elevation of the top of a tower from two distinct points ...
Text Solution
|
- The shadow of a tower standing on a level ground is found to be 40 m ...
Text Solution
|
- A vertical tower Stands on a horizontal plane and is surmounted by a v...
Text Solution
|
- if tantheta+sectheta=l then tantheta=
Text Solution
|
- If sin theta+ cos theta = p and sec theta + cosec theta = q; show that...
Text Solution
|
- If a sintheta + bcos theta = c, then prove that a costheta -b sintheta...
Text Solution
|
- Prove that (1+sectheta-tantheta)/(1+sectheta+tantheta) = (1-sintheta)/...
Text Solution
|
- The angle of elevation of the top of a tower 30 m high from the foot ...
Text Solution
|
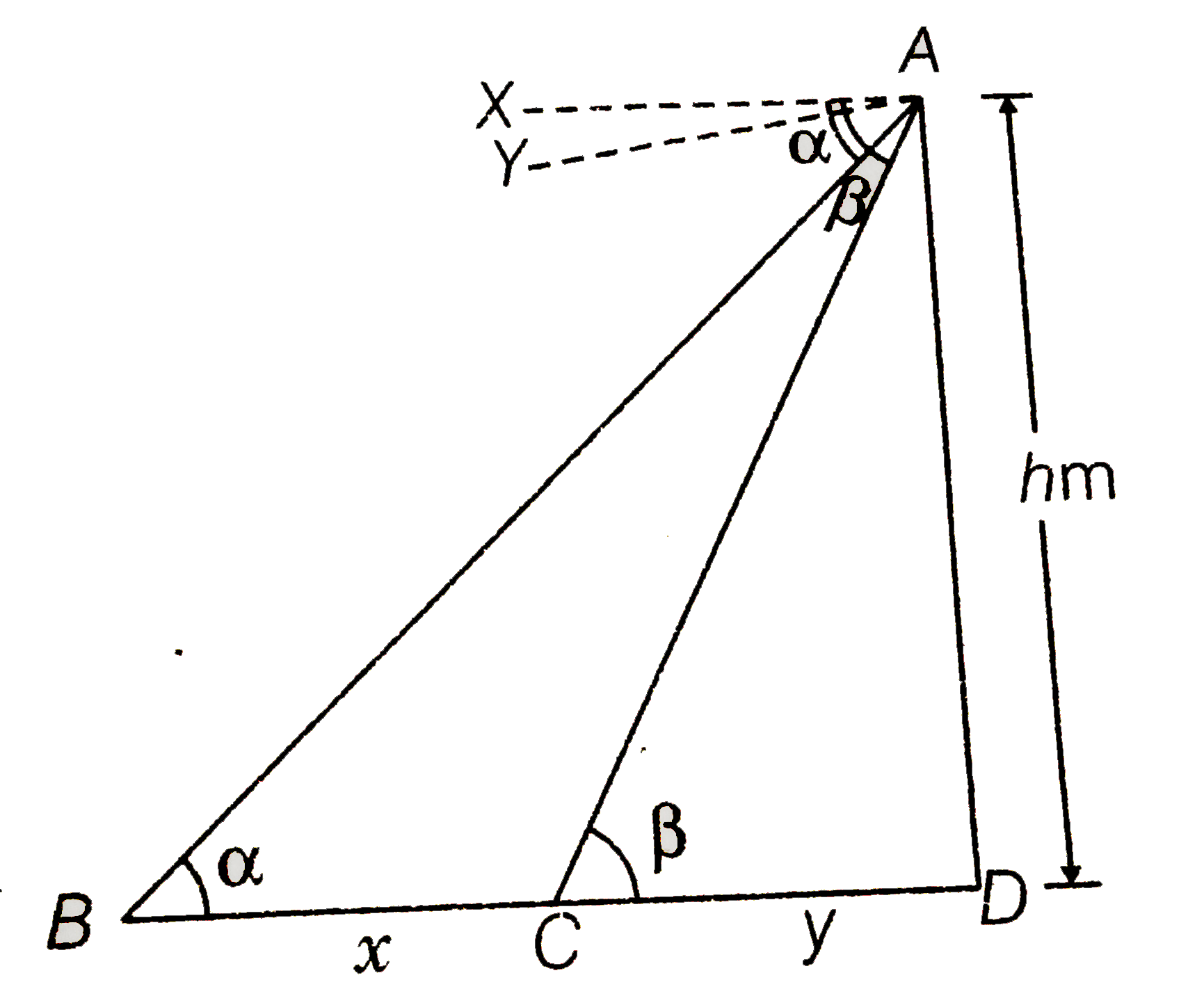
- From the top of a tower h m high, angles of depression of two objects,...
Text Solution
|
- A ladder rests against a vertical wall at inclination alpha to the hor...
Text Solution
|
- The angle of elevation of the top of a vertical tower from a point on ...
Text Solution
|
- From a window ( h meter above ground) the angle of elevation of other ...
Text Solution
|
- The lower window of a house is at a height of 2m above the ground and ...
Text Solution
|