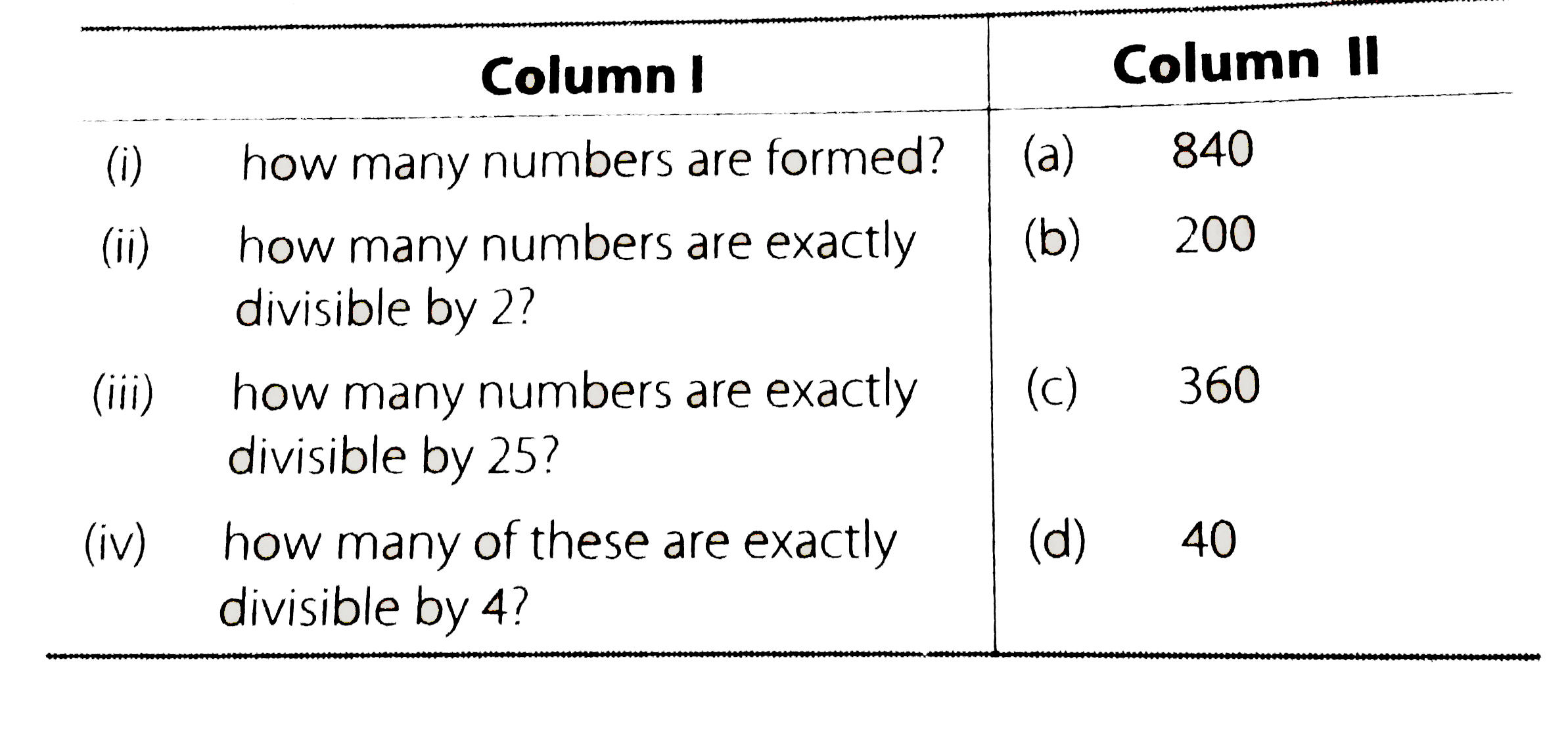Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-PERMUTATIONS AND COMBINATIONS-Matching The Columns
- There are 3 books of mathematics, 4 books of Physics and 5 on English....
Text Solution
|
- Five boys and five girls from a line. Find the number of ways of makin...
Text Solution
|
- There are 10 professors and 20 lecturers, out of whom a committee of 2...
Text Solution
|
- Using the digits 1, 2, 3, 4, 5, 6,7, a number of 4 different digits is...
Text Solution
|
- How many words (with or without dictionary meaning) can be made from t...
Text Solution
|