Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
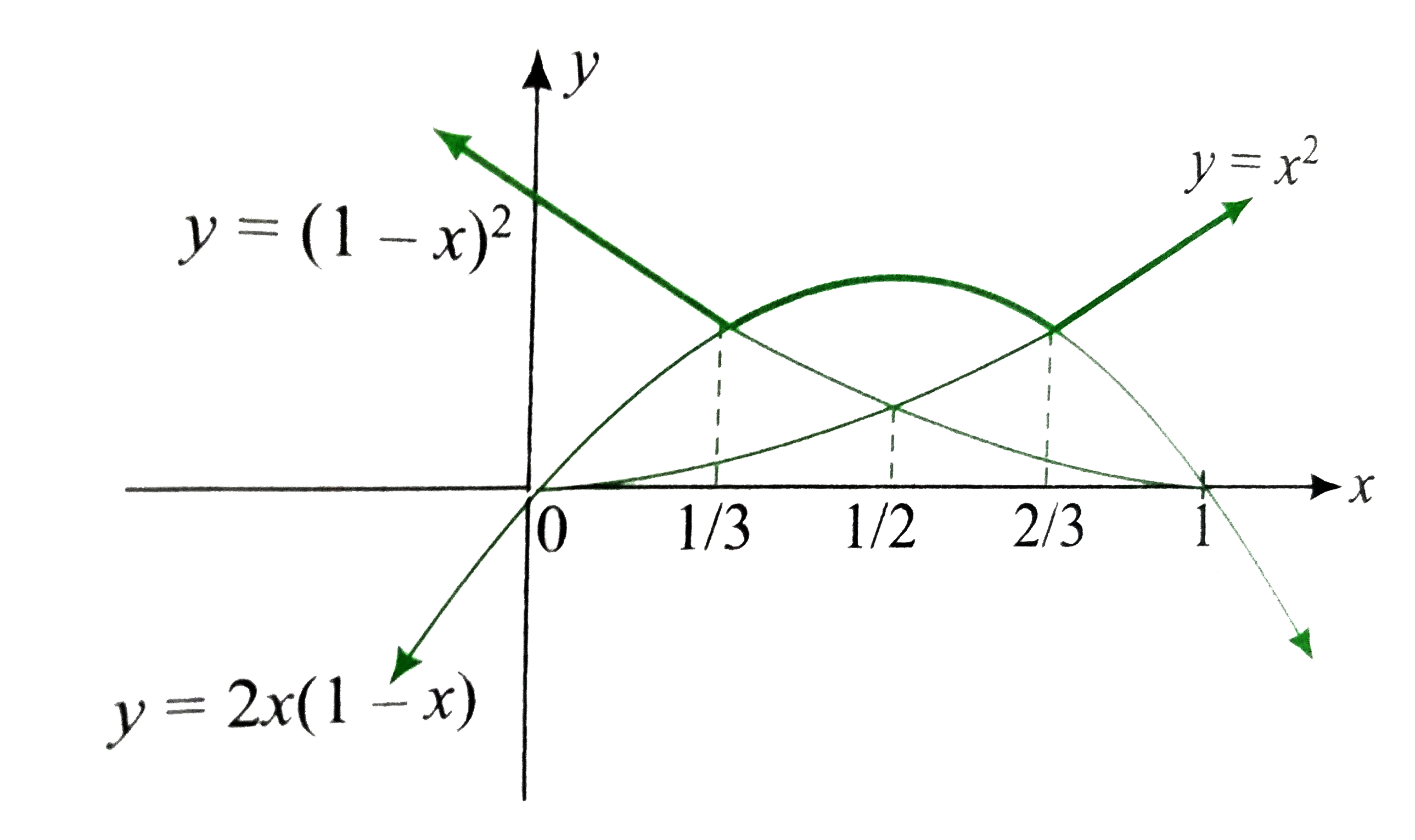
- Find the equivalent definition of f(x)=max{x^2,(1-x)^2,2x(1-x)}where ...
Text Solution
|
- If f(x)=m a xi mu m{x^3, x^2,1/(64)}AAx in [0,oo),t h e n f(x)={x^2,...
Text Solution
|
- Let f(x)=M a xi mu m{x^2,(1-x)^2,2x(1-x)}, where 0lt=xlt=1. Determin...
Text Solution
|
- Find the greatest and least values of function f(x)={-x ,\ \ \ \ -...
Text Solution
|
- The points of discontinuity of the function f(x)={2sqrt(x)\ \ \ ,\ \...
Text Solution
|
- If f: [0,3] to [0,3] is defined by: f(x) = {{:(1+x,0 le x le 2),(3-...
Text Solution
|
- Find (lim)(x->1)f(x) ,where f(x)={(x^2-1, xlt=1),(-x^2-1, x >1):}
Text Solution
|
- Find the equivalent definition of f(x)=max{x^2,(1-x)^2,2x(1-x)}where ...
Text Solution
|
- If f(x)=max{x^3, x^2,1/(64)}AAx in [0,oo),t h e n f(x)={x^2,0lt=xlt=...
Text Solution
|