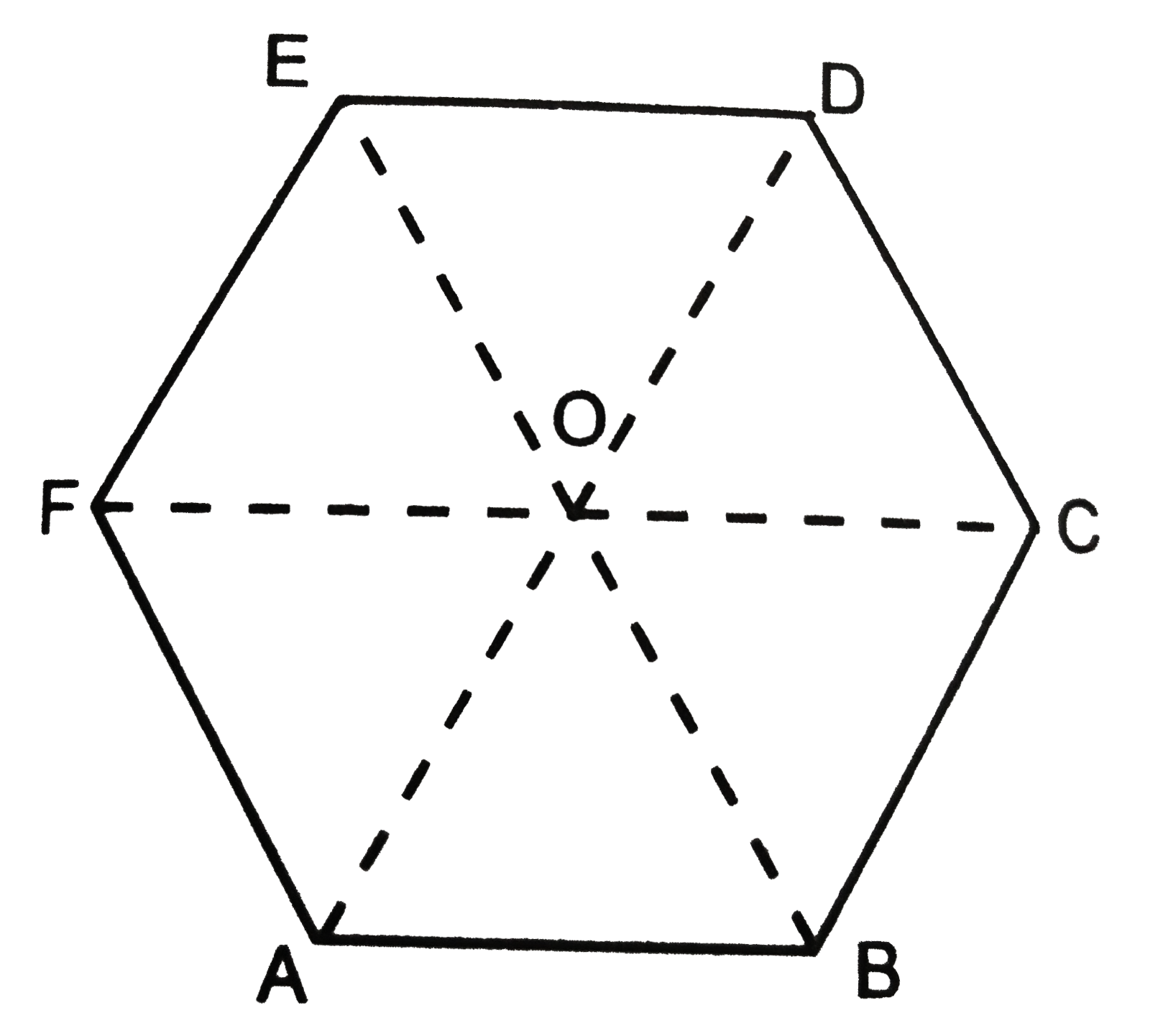
`ABCDEF` is a regular hexagon, Fig. 2 (c ) .65. What is the value of
` (vec (AB) + vec (AC) + vec (AD) + vec (AE) + vec (AF) ?`
.

ABCDEF is a regular hexagon with point O as centre. The value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF) is

In a regular hexagon ABCDEF,vec AE

In Fig. ABCDEF is a ragular hexagon. Prove that vec(AB) +vec(AC) +vec(AD) +vec(AE) +vec(AF) = 6 vec(AO) .

If ABCDE is a pentagon, then vec(AB) + vec(AE) + vec(BC) + vec(DC) + vec(ED) + vec(AC) is equal to

ABCD is a parallelogram Fig. 2 (c ) .64. AC and (BD) are its diagonals. Show that (a) vec (AC) +vec (BD) =2 vec (BC) (b) vec (AC) - vec (BD) =2 vec (AB) .

ABCDEF be a regular hexagon in the xy-plane and vec AB=4hat i then vec CD=

ABCDEF is a regular hexagon with centre a the origin such that vec(AB)+vec(EB)+vec(FC)= lamda vec(ED) then lamda = (A) 2 (B) 4 (C) 6 (D) 3

ABCDEF is a regular hexagon.Find the vector vec AB+vec AC+vec AD+vec AE+vec AF in terms of the vector vec AD

In a regular hexagon ABCDEF, prove that vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF)=3vec(AD)