Home
Class 12
PHYSICS
Find the relation between the three wave...

Find the relation between the three wavelengths `lamda1, lamda2and lamda3` from the energy level diagram shown below.

Text Solution

Verified by Experts

`E_c-E_B=(hc)/lamda_1" "...(1)`
`E_B-E_A=(hc)/lamda_2" " ...(2) `
`E_C-E_A=(hc)/lamda_3" "...(3)`
Adding (1) and (2), we have
`E_C-E_A=(hc)/lamda_1+(hc)/lamda_2" "...(4)`
From (3) and (4), we have
`(hc)/lamda_3=(hc)/lamda_1+(hc)/lamda_2rArr1/lamda_3=1/lamda_1+1/lamda_2`
`implieslamda_3=(lamda_1lamda_2)/(lamda_1+lamda_2)`
Promotional Banner

Topper's Solved these Questions

  • CBSE EXAMINATION PAPER - 2016

    CBSE COMPLEMENTARY MATERIAL|Exercise SECTION - E|17 Videos

  • CBSE EXAMINATION PAPER - 2016

    CBSE COMPLEMENTARY MATERIAL|Exercise SECTION - B|5 Videos

  • CBSE BOARD EXAMNATION PAPER (2017 )

    CBSE COMPLEMENTARY MATERIAL|Exercise SECTION E|12 Videos

  • CBSE Examination Paper Delhi–2014

    CBSE COMPLEMENTARY MATERIAL|Exercise SET-III (Questions Uncommon to set-I and II)|9 Videos

Similar Questions

Explore conceptually related problems

The relation between wavelength (lamda) and angular wave number (k) of a wave is

Due to transitions among its first three energy levels, hydrogenic atom emits radiation at three discrete wavelengths lamda_(1), lamda_(2), " and " lamda_(3) (lamda_(1) lt lamda_(2) lt lamda_(3)) . Then

Which curve shows the relation ship between the energy R and the wavelength lamda of a photon of electromagnetic radiation?

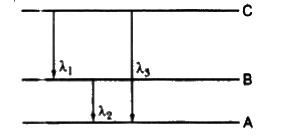
The energies E_1 and E_2 of two radiations are 25 eV and 50 e V respectively. The relation between their wavelengths, i.e., lamda_1 and lamda_2 will be.

The energy that should be added to an electron to reduce its de Broglie wavelength from lamda " to " lamda/2 is (Considering E to the energy of electron when its de Broglie wavelength is lamda )

Certain substance emits only the wavelengths lamda_1,lamda_2,lamda_3 and lamda_4 when it is at a high temperature, it will absorb only the following wavelengths

A dye absorbs a photon of wavelength lamda and re-emits the same energy into two photns of wavelength lamda_(1) and lamda_(2) respectively. The wavelength lamda is related to lamda_(1) and lamda_(2) as :

Neglecting the mass variation with velocity , the ratio of the wavelength ((lamda_e)/lamda_p) associated with an electron (lamda_e) having a kinetic energy E and wavelength associated with a Photon (lamda_p) having kinetie energy 4E is

The wavelength lamda_(e) of ann electron and lamda_(p) of a photon of same energy E are related by