Similar Questions
Explore conceptually related problems
Recommended Questions
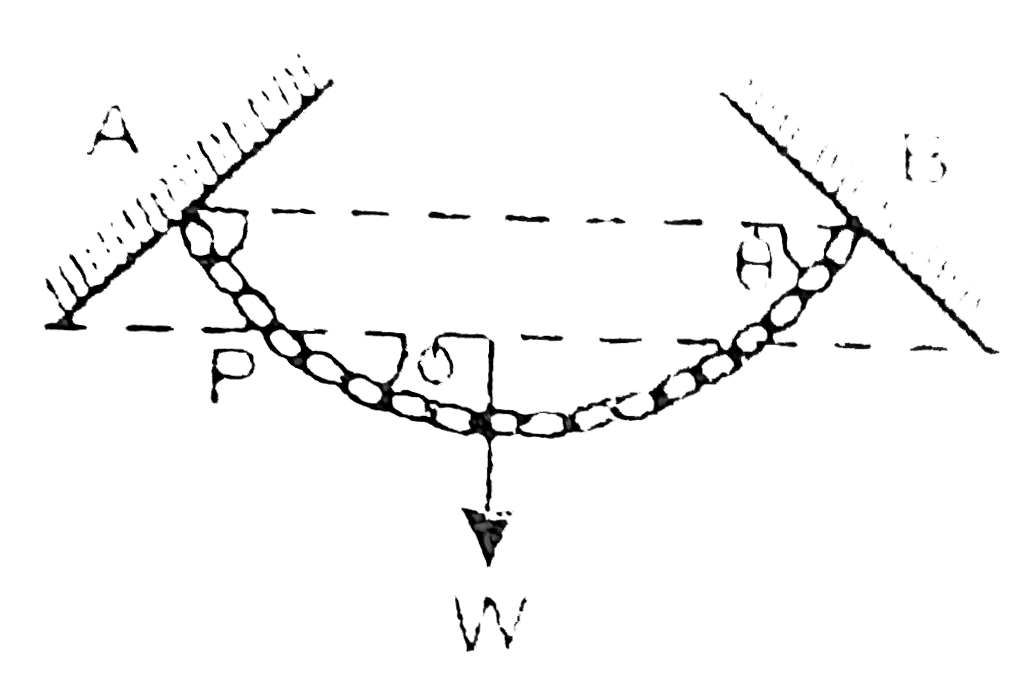
- A flexible chain of weight W hangs between two fixed points A and B at...
Text Solution
|
- A chain of mass 'm' is attached at two points A and B of two fixed wal...
Text Solution
|
- A flexible chain of weight W hangs between two fixed points A and B at...
Text Solution
|
- A chain of length L supported at the upper end is hanging vertically. ...
Text Solution
|
- A flexible chain of weight W hangs between two fixed points A and B at...
Text Solution
|
- In the arrangement shown in figure, coefficient of friction between tw...
Text Solution
|
- A flexible chain of weight W hangs between two fixed points A & B whic...
Text Solution
|
- A rough inclined plane is inclined at 30° to the horizontal as shown i...
Text Solution
|
- A rough inclined plane is inclined at 30° to the horizontal as shown i...
Text Solution
|