Home
Class 7
MATHS
In the given figure, two straight lines ...

In the given figure, two straight lines AB and CD intersect at a point such that `/_AOC = 50^(@)`. Find: (i) `/_BOD`
(ii) `/_BOC`

Text Solution

Verified by Experts

The correct Answer is:
`/_BOD = 50^(@)`
`/_BOC = 130^(@)`
Promotional Banner

Topper's Solved these Questions

  • CONSTRUCTIONS

    RS AGGARWAL|Exercise TEST PAPER (M.C.Q)|7 Videos

  • CONSTRUCTIONS

    RS AGGARWAL|Exercise TEST PAPER (Fill in the blanks)|5 Videos

  • CONSTRUCTIONS

    RS AGGARWAL|Exercise EXERCISE C(M.C.Q)|38 Videos

  • CONGRUENCE

    RS AGGARWAL|Exercise EXERCISE|18 Videos

  • DECIMALS

    RS AGGARWAL|Exercise TEST PAPER-3(D)|5 Videos

Similar Questions

Explore conceptually related problems

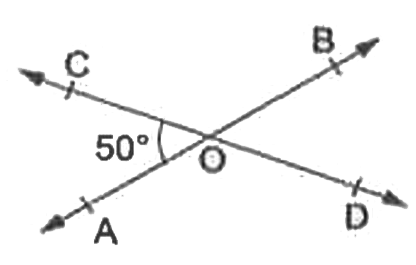
In the given figure, two straight lines AB and CD intersect at a point and /_ AOC = 50^(@) . Then, /_ BOD = ?

In the given figure, the two lines AB and CD intersect at a point O such that angleBOC=125^(@) . Find the values of x, y, and z.

In the given figure, three lines AB, CD and EF intersect at a point O such that angleAOE=35^(@) and angleBOD=40^(@) . Find the measure of angleAOC, angleBOF, angleCOF and angleDOE .

In the given figure,two straight line AB and CD intersect at a point O. If angleAOC=42^(@) ,Find the measure of each of the angles: angleAOD If angleAOC=42^(@) ,Find the measure of each of the angles: angleBOD If angleAOC=42^(@) ,Find the measure of each of the angles: anleCOB

Two lines AB and CD intersect at O .If " /_AOC=50^(@) , find /_AOD,/_BOD and /_BOC

In the given figure, AOB is a straight line and OC is a ray such that /_AOC = (3x+20)^(@) and /_BOC = (2x - 10)^(@) . Find the value of x and hence find (i) /_AOC (ii) /_BOC

In the given figure, straight lines AB and CD intersect at O.If angle beta = 3 angle p ,then angle p is equal to

In the figure, two chords AB and CD intersect each other at the point P. Prove that : AP. PB = CP. DP

In the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.

In the figure, diameter AB and chord CD intersect in point E. If m (arc CXB ) = 100^(@) . Find (i) /_ADC (ii) /_CDB (iii) /_ ACB