Topper's Solved these Questions
PARALLELOGRAMS
RS AGGARWAL|Exercise Exercise 16A|28 VideosPARALLELOGRAMS
RS AGGARWAL|Exercise Exercise 16B|10 VideosOPERATIONS ON ALGEBRAIC EXPRESSIONS
RS AGGARWAL|Exercise Exercise 6E (Tick the correct answer in each of the following:)|19 VideosPERCENTAGE
RS AGGARWAL|Exercise TEST PAPER -9 ( TRUE AND FALSE )|4 Videos
Similar Questions
Explore conceptually related problems
RS AGGARWAL-PARALLELOGRAMS-Exercise 16B
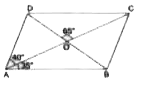
- In the adjoining figure , ABCD is a parallelogram in which angleCAD=4...
Text Solution
|
- The two diagonals are not necessarily equal in a
Text Solution
|
- The lengths of the diagonals of a rhombus are 16 cm and 12 cm . The le...
Text Solution
|
- Two adjacent angles of a parallelograms are (2x+25)^@ and (3x-5)^@ . ...
Text Solution
|
- The diagonals do not necessarily intersect at right angles in a
Text Solution
|
- The length and breadth of a rectangle are in the ratio 4:3. If the d...
Text Solution
|
- The bisectors of any two adjacent angles of a parallelogram intersect ...
Text Solution
|
- If an angle of a parallelogram is two-thirds of its adjacent angle, th...
Text Solution
|
- The diagonals do not necessarily bisect the interior angles at the ver...
Text Solution
|
- In a square ABCD, AB=(2x+3) cm and BC=(3x-5) cm . Then , the value of ...
Text Solution
|
- If one angle of a parallelogram is 24^@ less than twice the smallest ...
Text Solution
|