Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-APPLICATION OF DERIVATIVES-Application Of Derivatives
- Using differentials, find the approximate value of (1. 999)^5
Text Solution
|
- Find the approximate volume of metal in a hollow spherical shell wh...
Text Solution
|
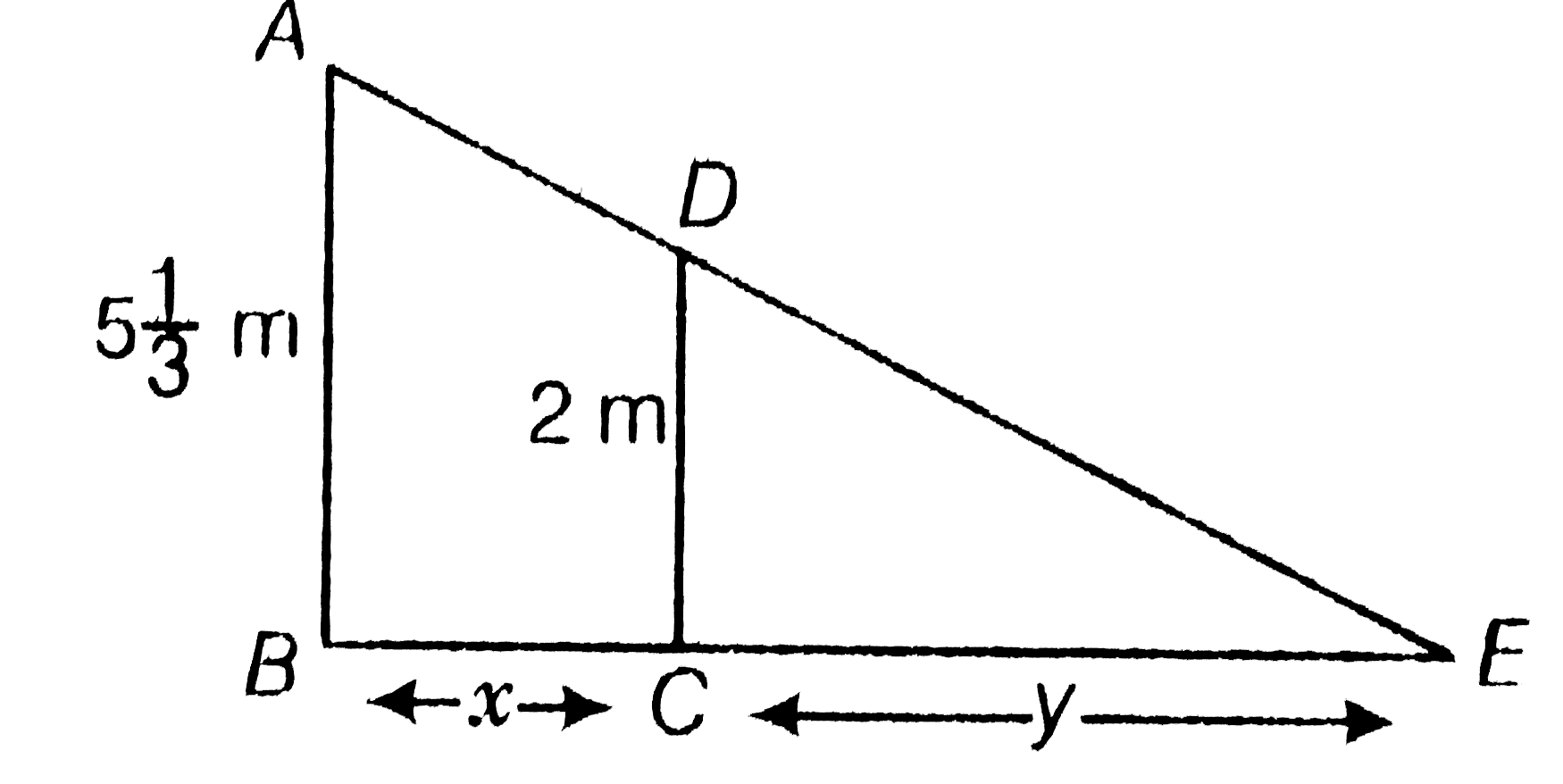
- A man 2m tall, walks at the rate of 1 2/3m//s e c towards a street lig...
Text Solution
|
- A swimming pool is to be drained by cleaning. If L represents the n...
Text Solution
|
- The volume of a cube is increasing at a constant rate. Prove that the ...
Text Solution
|
- xa n dy are the sides of two squares such that y=x-x^2 . Find the rate...
Text Solution
|
- Prove that the curve y = x^2 and xy = k intersect orthogonally if 8k^2...
Text Solution
|
- Prove that the curves x y=4a n dx^2+y^2=8 touch each other.
Text Solution
|
- Find the required point be P(x1, y1)dot The tangent to the curve sqrt(...
Text Solution
|
- Find the angle of intersection of the curves y=4-x^(2) and y=x^(2)
Text Solution
|
- Prove that the curves y^2=4xa n dx^2+y^2-6x+1=0 touch each other at th...
Text Solution
|
- Find the equation(s) of normal(s) to the curve 3x^2-y^2=8 which is (ar...
Text Solution
|
- At what points on the curve x^2+y^2-2x-4y+1=0 , the tangents are paral...
Text Solution
|
- Show that the line d/a+y/b=1 touches the curve y=b e^(-x/a) at the poi...
Text Solution
|
- Show that f(x) = 2x + cot^-1 x + log(sqrt(1+x^2)-x) is increasing in R
Text Solution
|
- Show that for alt=1,f(x)=sqrt(3) si nx-cosx-2a x+b is decreasing on ...
Text Solution
|
- Show that f(x)=tan^(-1)(sinx+cosx) is an increasing function on the ...
Text Solution
|
- At what points, the slope of the curve y=-x^3+3x^2+9x-27 at point (...
Text Solution
|
- Prove that f(x)=sinx+sqrt(3)cosx has maximum value at x=pi/6 .
Text Solution
|
- If the sum of lengths of hypotenuse and a side of a right angled tr...
Text Solution
|