Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-APPLICATION OF DERIVATIVES-Application Of Derivatives
- At what points, the slope of the curve y=-x^3+3x^2+9x-27 at point (...
Text Solution
|
- Prove that f(x)=sinx+sqrt(3)cosx has maximum value at x=pi/6 .
Text Solution
|
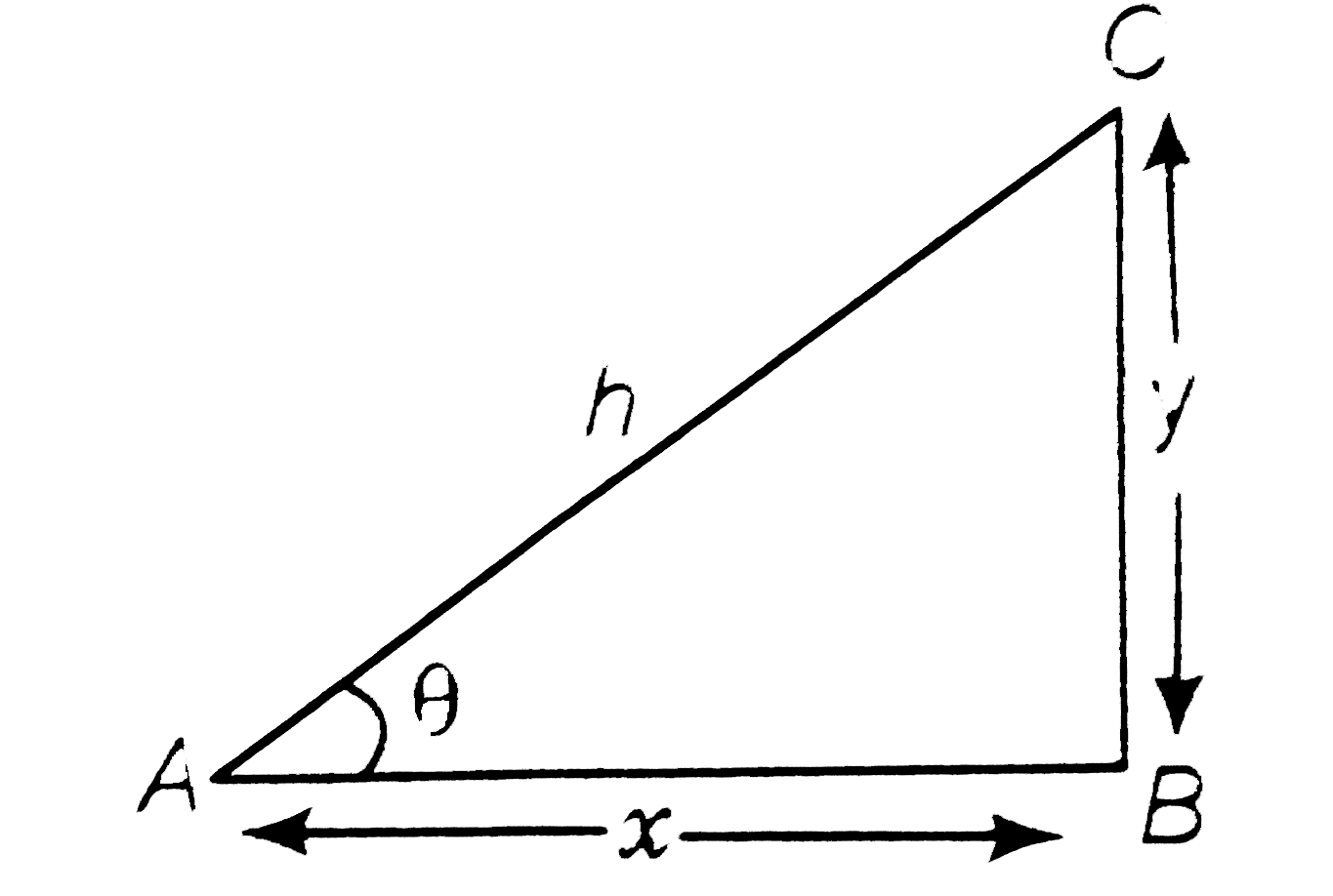
- If the sum of lengths of hypotenuse and a side of a right angled tr...
Text Solution
|
- Find the points of local maxima, local minima and the points of inf...
Text Solution
|
- A telephone company in a town has 500 subscribers on its list and c...
Text Solution
|
- If the straight line xcosalpha+ysinalpha=p touches the curve (x^2)/(a^...
Text Solution
|
- An open box with a square base is to be made out of a given quantit...
Text Solution
|
- Find the dimensions of the rectangle of perimeter 36cm which will s...
Text Solution
|
- The sum of the surface areas of a sphere and a cube is given. Show tha...
Text Solution
|
- A B is a diameter of a circle and C is any point on the circle. ...
Text Solution
|
- A metal box with a square base and vertical sides is to contain 102...
Text Solution
|
- The sum of the surface areas of the rectangular parallelopiped with...
Text Solution
|
- The sides of an equilateral triangle are increasing at the rate of ...
Text Solution
|
- A ladder 5 m long is leaning against a wall. The bottom of the ladder ...
Text Solution
|
- The curve y= x^(1/5) has at (0, 0)
Text Solution
|
- Find the equation(s) of normal(s) to the curve 3x^2-y^2=8 which is (ar...
Text Solution
|
- If the curves ay+x^2=7 and x^3=y cut orthogonally at (1, 1) then a= ...
Text Solution
|
- If y=x^4-12 and if x changes from 2 to 1.99. what is the appoinmate ch...
Text Solution
|
- Find the equation of the tangent to the curve (1+x^2)y=2-x , where it ...
Text Solution
|
- The points at which the tangents to the curve y=x^(3)-12x+18 are paral...
Text Solution
|