A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-KVPY-exercise
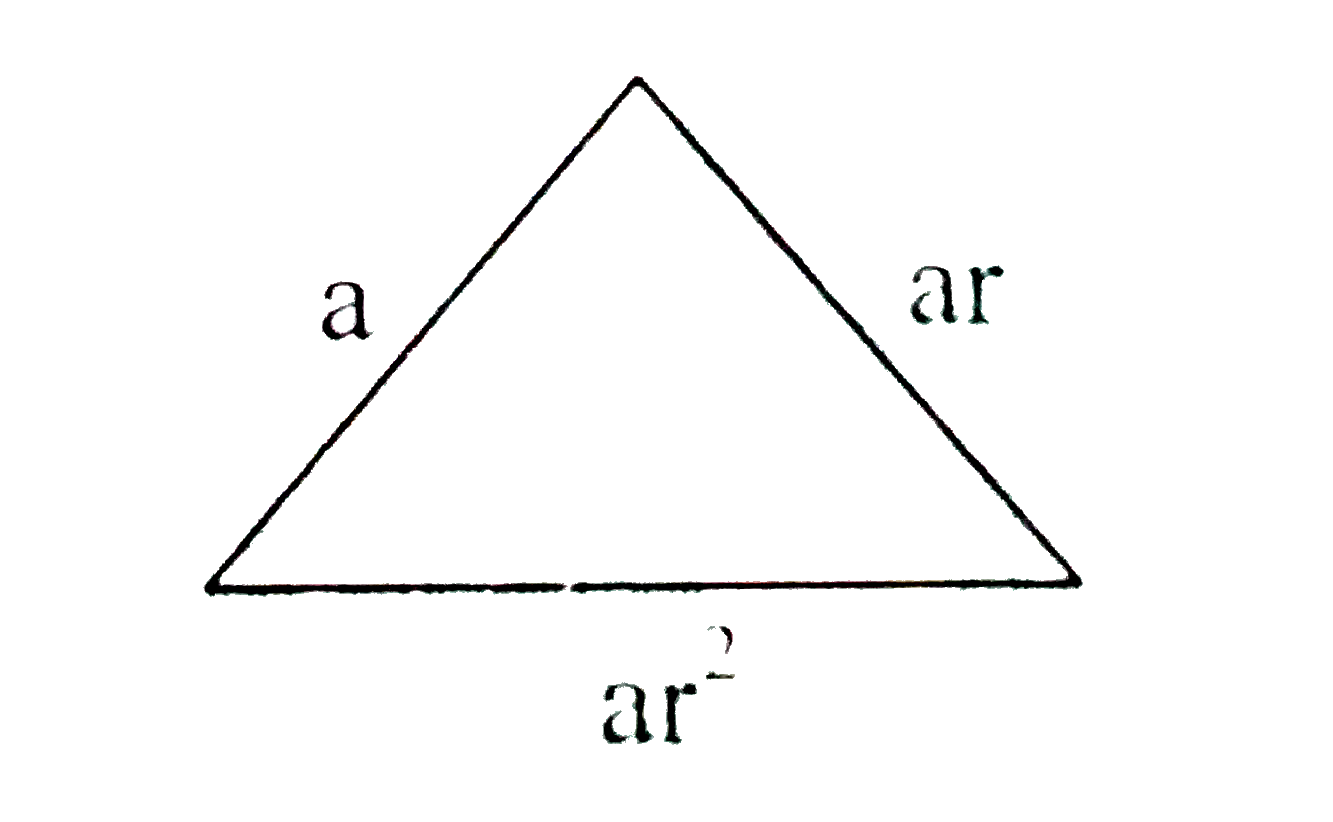
- Suppose the sides of a triangle form a geometric progression with ...
Text Solution
|
- The number of ordered pairs of integers(x,y) which satisfy x^3 + y^3 =...
Text Solution
|
- A,B,E are 3 points of the circumference of a circle of radius 1. If an...
Text Solution
|
- [x^2] = x + 1 how many real roots
Text Solution
|
- If x + y = 1 where x and y are positive numbers, then the minimum valu...
Text Solution
|
- If all the natural numbers from 1 to 2021 are written as 12345.....202...
Text Solution
|
- [(2^(2020)+1)/(2^(2018)+1)] + [(3^(2020)+1)/(3^(2018)+1)] + [(4^(2020)...
Text Solution
|
- Let's say abcde is a 5 digit number which when multiplied by 9 new num...
Text Solution
|
- I: m is any composite number that divides (m-1)! II: n is a natural ...
Text Solution
|
- 2^x + 3^y = 5^(xy) Number of solutions = ?
Text Solution
|
- In a book self if m books have black cover and n books have blue cover...
Text Solution
|
- xgt2ygt0 and 2log(x-2y)=log xy Possible values of x/y is/are
Text Solution
|
- In an equiangular octagon if 6 consecutive sides are 6,8,7,10,9,5 then...
Text Solution
|
- If the function f(x) = 2+x^2-e^x and g(x) = f^(-1)(x), then the value ...
Text Solution
|
- S= lim(nrarroo) sum(k=0)^n 1/sqrt(n^2 + k ^2)
Text Solution
|
- f(x): R to R |f(x)-f(y)| > |x-y| forall x,y in R check one-one/man...
Text Solution
|
- x^3 - [x]^3 = (x - [x])^3
Text Solution
|
- S1:lim(n->oo) (2^n + (-2)^n)/2^n does not exist S2:lim(n->oo) (3^n +...
Text Solution
|
- In a 15 sidead polygon a diagnol is chosen at random. Find the probabi...
Text Solution
|