Home
Class 12
MATHS
Let ABC be a triangle and P be a point...

Let ABC be a triangle and P be a point inside ABC such that ` vec(PA) + 2vec(PB) + 3vec(PC) = vec0`. The ratio of the area of triangle ABC to that of APC is - (A) ` 2` (B) ` 3/2`(C) `5/3` (D) `3`

A

`2`

B

`3/2`

C

`5/3`

D

`3`

Text Solution

Verified by Experts

The correct Answer is:
D

`vec(PA) + 2vec(PB) + 3vec(PC) = 0`
`(veca - vecp) + 2(vecb- vecp) + 3(vecc - vecp) = 0`
`vecp = (veca + 2vecb + 3vecc)/(6)`
`("Area"DeltaABC)/( "Area" DeltaAPC) = (1/2|vecaxxvecb+vecbxxvecc+veccxxveca|)/(1/2|vecaxxvecp+vecpxxvecc+veccxxveca|)`
put `vecp = (veca+2vecb+3vecc)/(6)`
ratio `= 3`
Promotional Banner

Topper's Solved these Questions

  • KVPY

    KVPY PREVIOUS YEAR|Exercise PART-I MATHEMATICS|15 Videos

  • KVPY

    KVPY PREVIOUS YEAR|Exercise PART-2 MATHEMATICS|5 Videos

  • KVPY 2021

    KVPY PREVIOUS YEAR|Exercise PART II MATHEMATICS|4 Videos

Similar Questions

Explore conceptually related problems

Let O be an interior point of triangle ABC, such that 2vec(OA)+3vec(OB)+4vec(OC)=0 , then the ratio of the area of DeltaABC to the area of DeltaAOC is

If P is a point inside Delta ABC such that BC(vec PA)+CA(vec PB)+AB(vec PC)=vec O then P is the .....

Let O be an interior point of Delta ABC such that 2vec OA+5vec OB+10vec OC=vec 0

Let vec(A)D be the angle bisector of angle A" of " Delta ABC such that vec(A)D=alpha vec(A)B+beta vec(A)C, then

G is a point inside the plane of the triangle ABC,vec GA+vec GB+vec GC=0, then show that G is the centroid of triangle ABC.

For any four points A,B,C,D |vec (AB) xx vec (CD)-vec (BC) xx vec (AD)+vec (CA) xx vec (BD)| is equal to 4 times the area of triangle- (1) ABC (2) BCD (3) ACD (4) ABD

If D is the mid-point of the side BC of a triangle ABC, prove that vec AB+vec AC=2vec AD .

ABC is a triangle and P any point on BC.if vec PQ is the sum of vec AP+vec PB+vec PC ,show that ABPQ is a parallelogram and Q, therefore,is a fixed point.

If D is the mid point of side BC of a triangle ABC such that vec AB+vec AC=lambdavec AD, write the value of lambda

KVPY PREVIOUS YEAR-KVPY-exercise
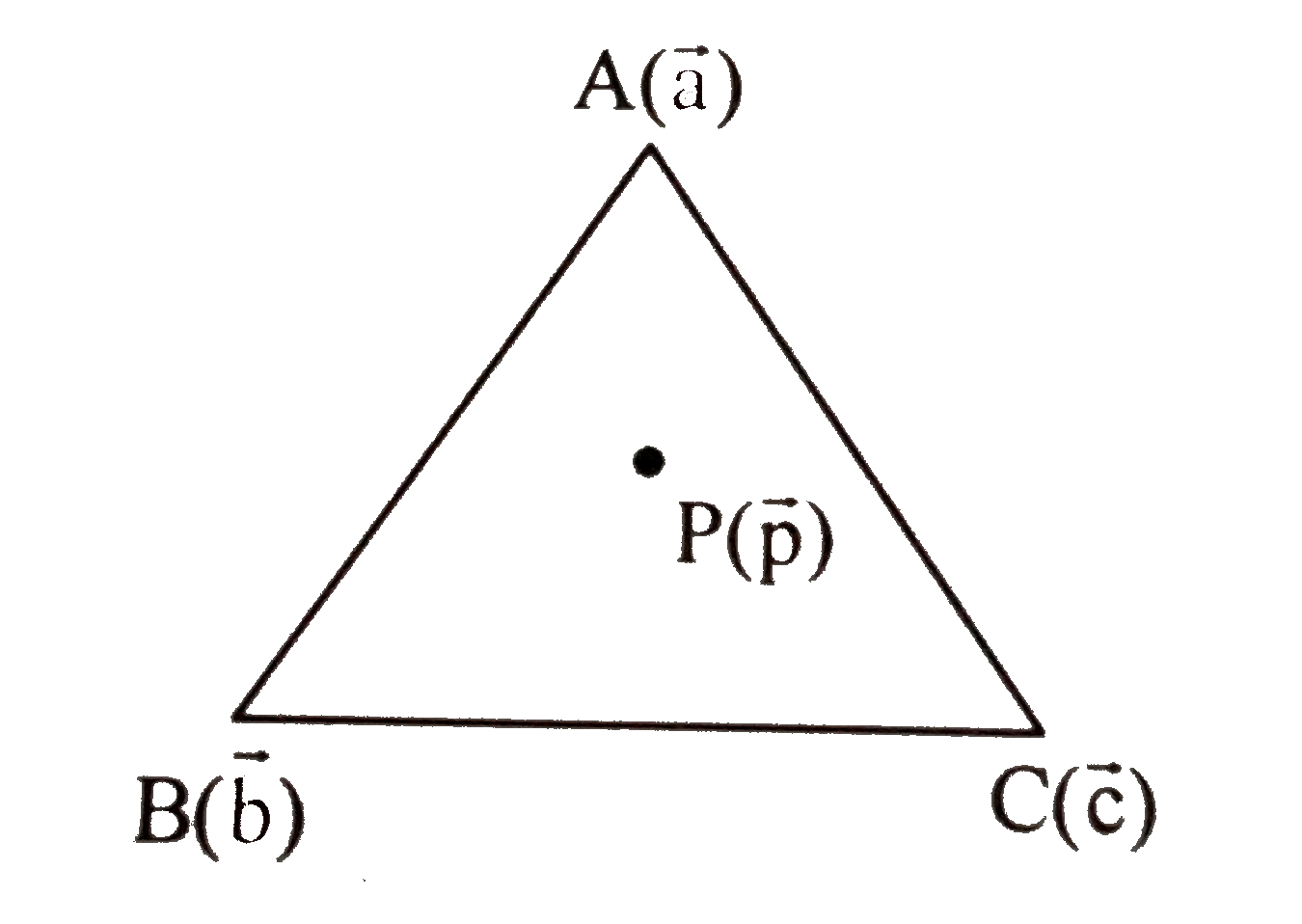
  1. Let ABC be a triangle and P be a point inside ABC such that vec(PA...

    Text Solution

    |

  2. The number of ordered pairs of integers(x,y) which satisfy x^3 + y^3 =...

    Text Solution

    |

  3. A,B,E are 3 points of the circumference of a circle of radius 1. If an...

    Text Solution

    |

  4. [x^2] = x + 1 how many real roots

    Text Solution

    |

  5. If x + y = 1 where x and y are positive numbers, then the minimum valu...

    Text Solution

    |

  6. If all the natural numbers from 1 to 2021 are written as 12345.....202...

    Text Solution

    |

  7. [(2^(2020)+1)/(2^(2018)+1)] + [(3^(2020)+1)/(3^(2018)+1)] + [(4^(2020)...

    Text Solution

    |

  8. Let's say abcde is a 5 digit number which when multiplied by 9 new num...

    Text Solution

    |

  9. I: m is any composite number that divides (m-1)! II: n is a natural ...

    Text Solution

    |

  10. 2^x + 3^y = 5^(xy) Number of solutions = ?

    Text Solution

    |

  11. In a book self if m books have black cover and n books have blue cover...

    Text Solution

    |

  12. xgt2ygt0 and 2log(x-2y)=log xy Possible values of x/y is/are

    Text Solution

    |

  13. In an equiangular octagon if 6 consecutive sides are 6,8,7,10,9,5 then...

    Text Solution

    |

  14. If the function f(x) = 2+x^2-e^x and g(x) = f^(-1)(x), then the value ...

    Text Solution

    |

  15. S= lim(nrarroo) sum(k=0)^n 1/sqrt(n^2 + k ^2)

    Text Solution

    |

  16. f(x): R to R |f(x)-f(y)| > |x-y| forall x,y in R check one-one/man...

    Text Solution

    |

  17. x^3 - [x]^3 = (x - [x])^3

    Text Solution

    |

  18. S1:lim(n->oo) (2^n + (-2)^n)/2^n does not exist S2:lim(n->oo) (3^n +...

    Text Solution

    |

  19. In a 15 sidead polygon a diagnol is chosen at random. Find the probabi...

    Text Solution

    |