A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
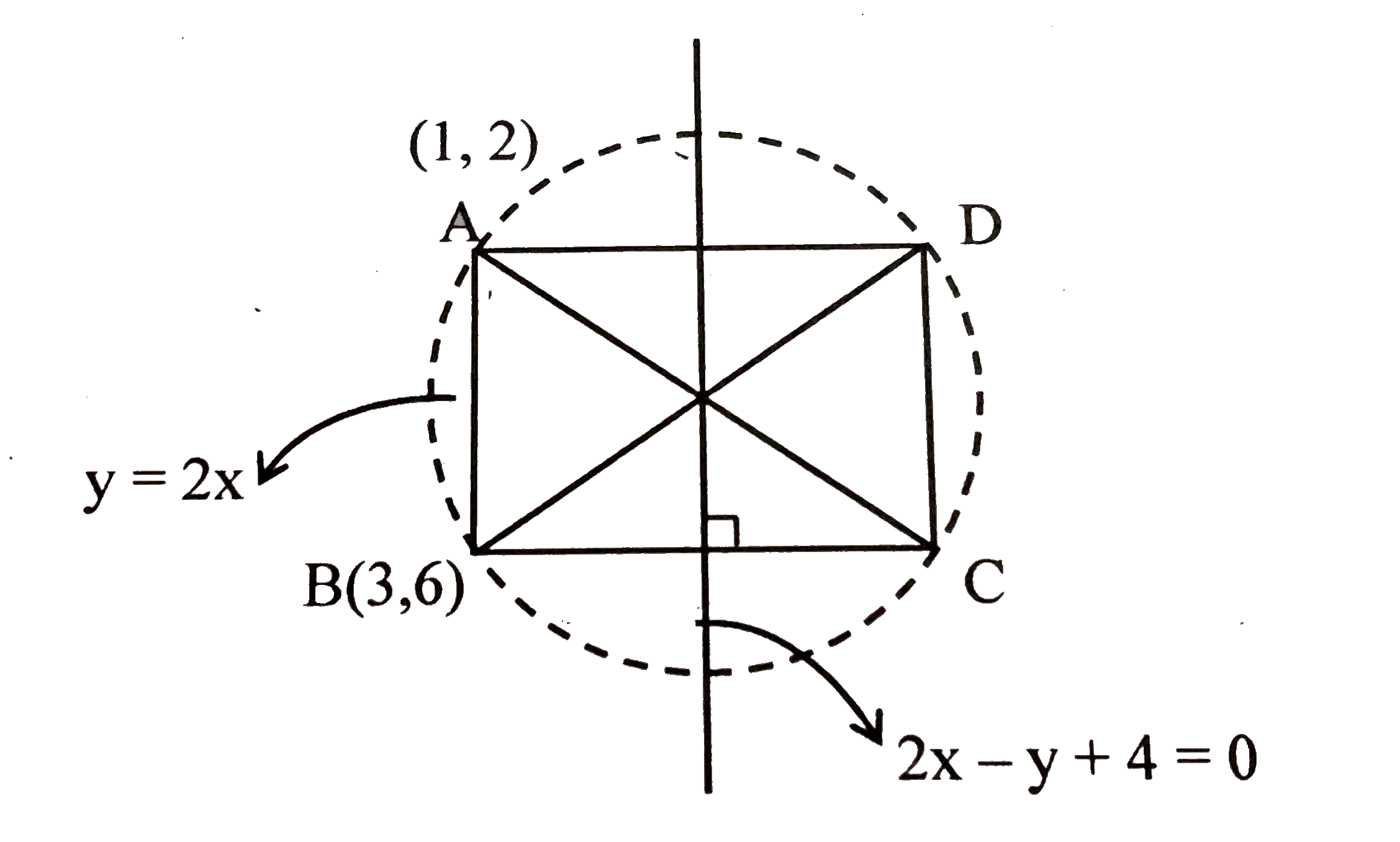
- In a recatngle ABCD, the coordinates of A and B are (1, 2) and (3, 6) ...
Text Solution
|
- One of the diameter of a circle circumscribing the rectangle ABCD is 4...
Text Solution
|
- One of the diameters of the circle circumscribing the rectangle ABCD i...
Text Solution
|
- 2x-y+4=0 is a diameter of a circle which circumscribes a rectangle ABC...
Text Solution
|
- One of the diameters of circle circumscribing the rectangle ABCD is4y=...
Text Solution
|
- In a recatngle ABCD, the coordinates of A and B are (1, 2) and (3, 6) ...
Text Solution
|
- One of the diameters of the circle circumscribing the rectangle ABCD i...
Text Solution
|
- आयत ABCD के परिवृत्त के व्यास का समीकरण 4y=x+7 है। यदि A तथा B क्रमशः ...
Text Solution
|
- ABCD is a rectangular A circle circumscribing the rectangle. The coord...
Text Solution
|