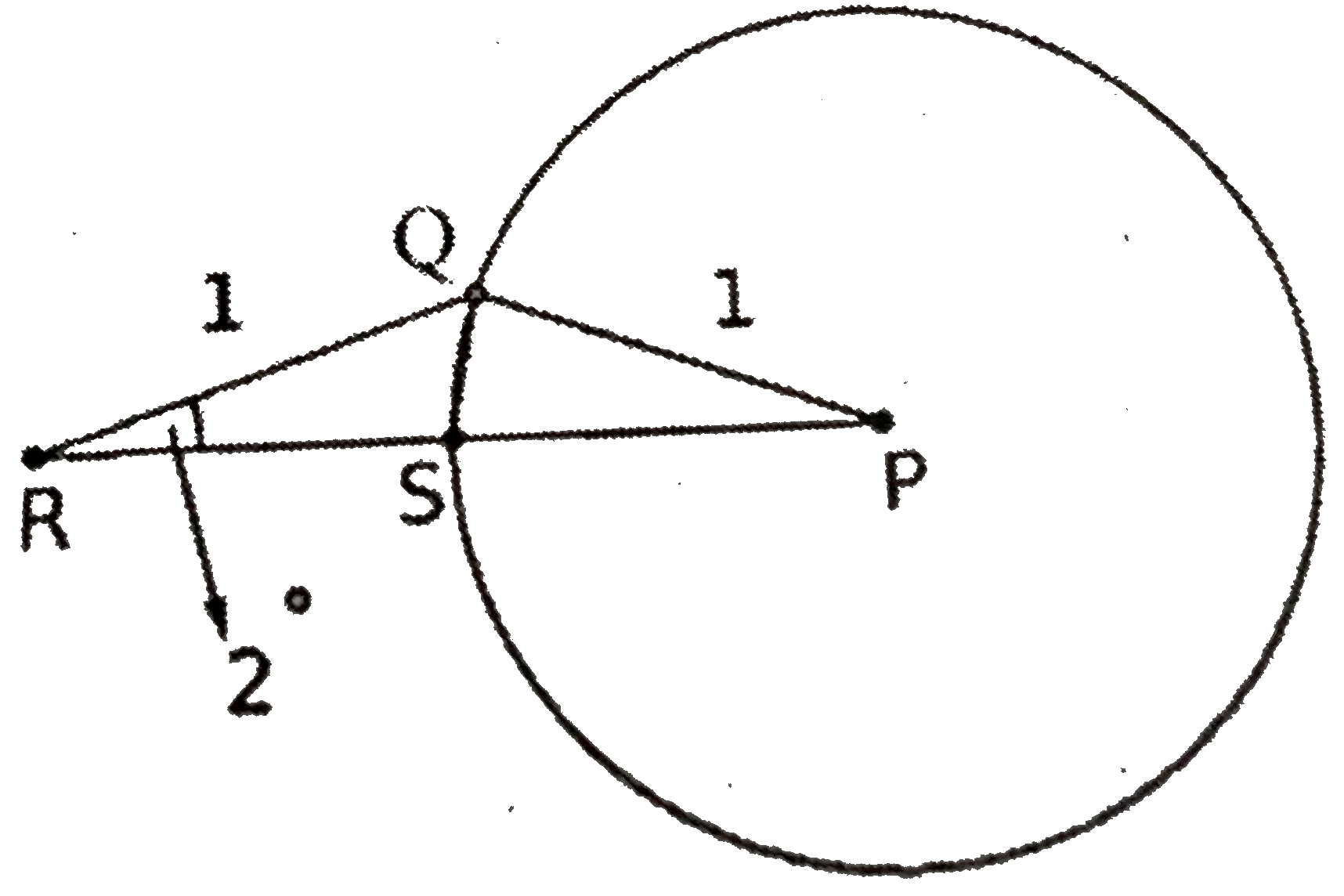A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-KVPY-PART-I MATHEMATICS
- Let f(x) be a quadratic polynomial with f(2)=-2. Then the coefficient ...
Text Solution
|
- The square root of (0.75)^(3)/(1-(0.75))+(0.75+(0.75)^(2)+1) is-
Text Solution
|
- The side of a triangle are distinct integers in an arithmetic progress...
Text Solution
|
- If a, b, c, d are positive real numbers such that (a)/(3)=(a+b)/(4)=(a...
Text Solution
|
- For (2^(2)+4^(2)+6^(2)+.......+(2n)^(2))/(1^(2)+3^(2)+......+(2n-1)^(2...
Text Solution
|
- In triangle ABC, let AD, BE and CF be the internal angle bisectors wit...
Text Solution
|
- A regular octagon is formed by cutting congruent isosceles right-angle...
Text Solution
|
- A circle is drawn in a sector of a larger circle of radius r, as shown...
Text Solution
|
- In the figure AHKF, FKDE and HBCK are unit squares, AD and BF intersec...
Text Solution
|
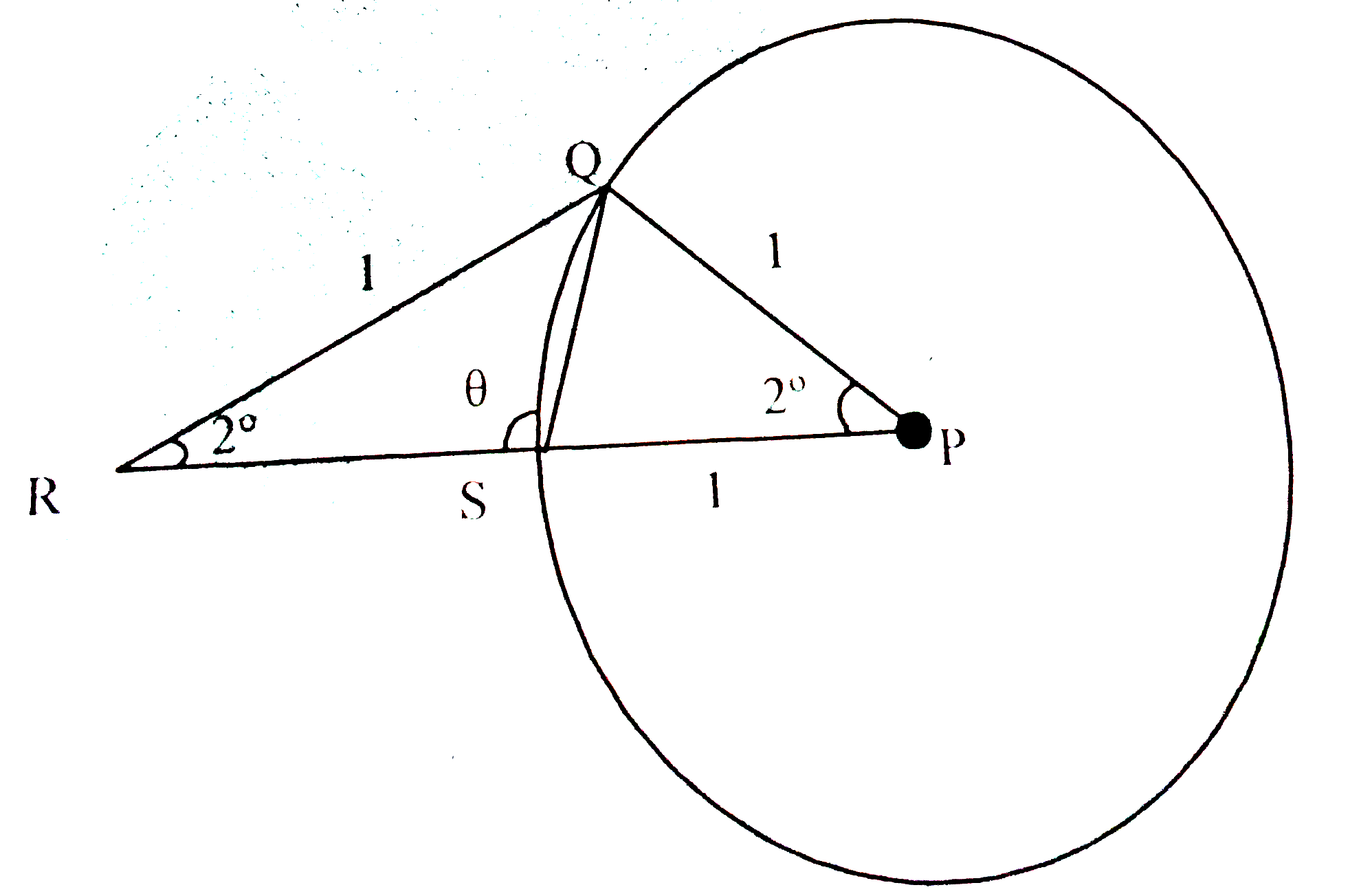
- Suppose Q is a point on the circle with center P and radius 1, as show...
Text Solution
|
- Observe that, at any instant, the minute and hour hands of a clock ma...
Text Solution
|
- Two workers A and B are engaged to do a piece of work. Working alone, ...
Text Solution
|
- When a bucket is half full, the weight of the bucket and the water is ...
Text Solution
|
- How many ordered pairs of (m,n) integers satisfy (m)/(12)=(12)/(n)?
Text Solution
|
- Let S = {1,2,3,..., 40} and let A be a subset of S such that notwo ele...
Text Solution
|