Home
Class 12
MATHS
Let P be an interior point of a tr...

Let P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then `angle A ` equals -

A

`30^(@)`

B

`60^(@)`

C

`90^(@)`

D

`120^(@)`

Text Solution

Verified by Experts

The correct Answer is:
C

` 2theta +2alpha = 180^(@)`
`implies theta+alpha=90^(@)`
`implies angle A=90^(@)`
Promotional Banner

Similar Questions

Explore conceptually related problems

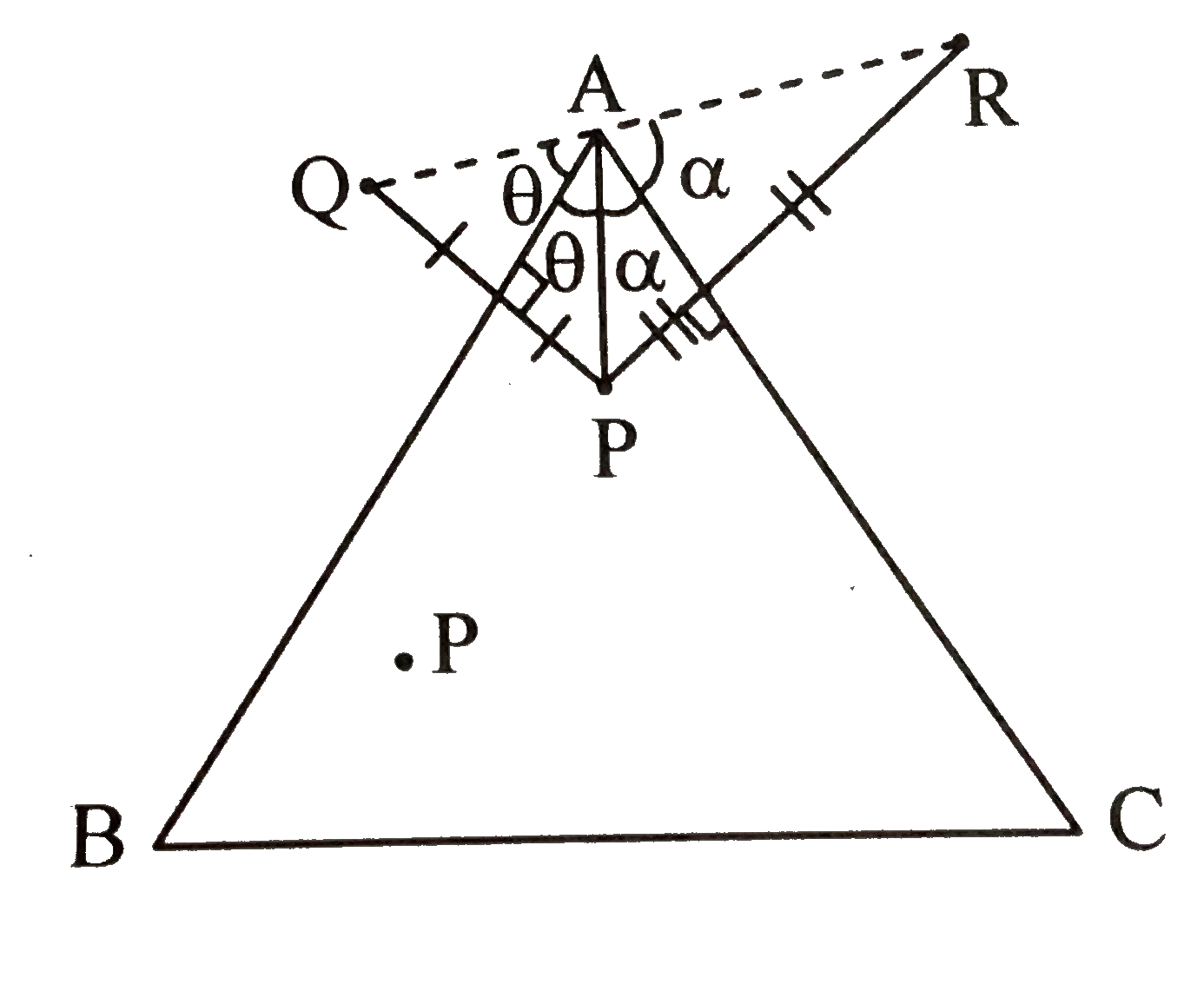
Let P be an interior point of a triangle ABC. Let Q andR be the reflections of P in AB and AC, respectively.If Q,A,R are collinear then ZA equalsB.60^(@)D.120^(@)30^(@)90^(@)

P,Q and R are three points with position vector i+j,i-j and ai +bj+ck respectively.if P,Q,R are collinear then

P,Q and R are three points with position vector i + j , i - j and ai +bj +ck respectively. if P,Q,R are collinear then

In a ? ABCD , AB | | DC. P and Q are the mid-points of AB and DC respectively AC, BD meet at O.Show that P , O , Q are collinear.

In a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR

Let P be a point inside a triangle ABC with /_ABC=90^(@) . Let P_(1) and P_(2) be the images of P under reflection in AB and BC respectively. The distance between the circumcenters of triangles ABC and P_(1) P_(2) is

P is an interior point of an equilateral triangle ABC. If P equidistant from AB and BC, BC and AC, then /_ BPC = _____

The sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P Q,and R respectively.

Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a

If DeltaABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-