Home
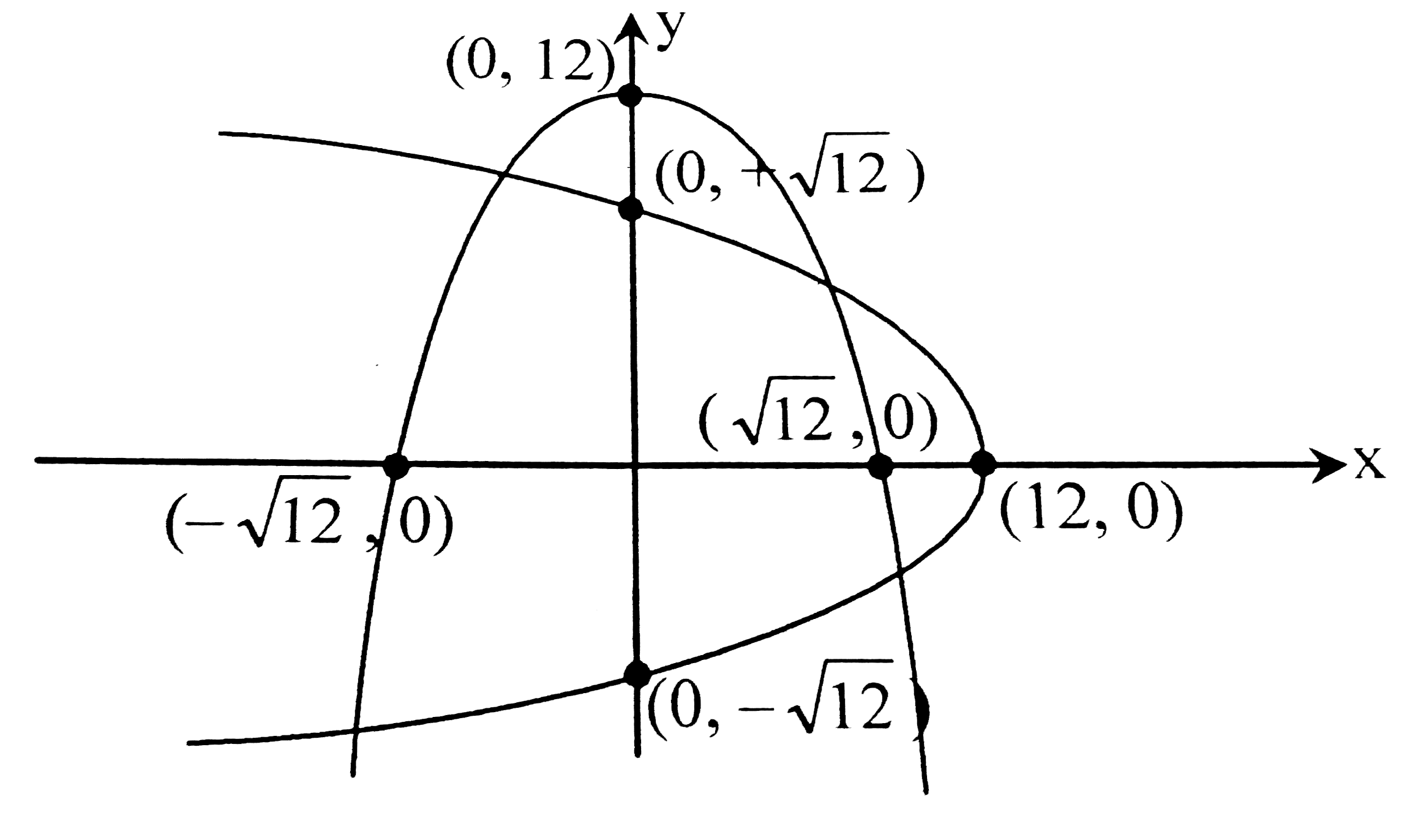
Class 12
MATHS
The number of ordered pairs (x,y) of rea...

The number of ordered pairs (x,y) of real numbers that satisfy the simultaneous equations
`x+y^(2)=x^(2)+y=12` is

A

0

B

1

C

2

D

4

Text Solution

Verified by Experts

The correct Answer is:
D
`x+y^(2)=x^(2)+y=12`
`"curve"(1)x+y^(2)=12" ""curve"(2)x^(2)+y=12`
`y^(2)=-(x-12)" "x^(2)=-(y-12)`
Intersection on x-axis (2,0) Intersection on x-axis `=(+-sqrt(12),0)`
Intersection on y-zxis `(0,+-sqrt(12))" "Intersection on y-axis =(0,12)`

four intersection
Promotional Banner

Similar Questions

Explore conceptually related problems

The number of ordered pair(s) (x, y) of real numbers satisfying the equation 1+x^(2)+2x sin(cos^(-1)y)=0 , is :

Find all ordered pairs of real numbers that satisfy both the equations x^(2)+y^(2)=2xy and x^(2)+y^(2)=6x+6y+2

The number of ordered pairs (x,y) of real number satisfying 4x^(2)-4x+2=sin^(2)y and x^(2)+y^(2)<=3 equal to

The number of ordered pairs (x, y) of integers satisfying x^3 + y^3 = 65 is

Find the number of ordered pairs (x,y) of integers which satisfies the following system of equations X^(x+y)=Y^(12)y^(y+x)=X^(3)

Number of pairs (x,y) real number that satisfy 2x^(2)+y^(2)+2xy-2y+2=0, is

The number of ordered pairs of positive integral (x,y) , that satisfy the equation (1)/(x)+(1)/(y)=(1)/(2004)

The number of all possible ordered pairs (x, y), x, y in R satisfying the system of equations x + y = (2pi)/(3), cos x + cos y = (3)/(2) is

The number of all possible ordered pairs (x, y) x, y in R satisfying the system of equations x + y = (2pi)/(3), "cos" x + "cos" y = (3)/(2), is